Series of Activities on Number Systems
Introduction
Our daily life is based on numbers. We use it for shopping, reckoning the time, counting distances and so on. Simple calculations seem effortless and trivial for most of our necessities.So we should know about numbers. Numbers help us count concrete objects. They help us to say which collection of objects . In this we are learning about basic operations of numbers - different types of numbers, representation, etc.

How can math be so universal? First, human beings didn't invent math concepts; we discovered them.
Also, the language of math is numbers, not English or German or Russian.
If we are well versed in this language of numbers, it can help us make important decisions and perform everyday tasks.
Math can help us to shop wisely, understand population growth, or even bet on the horse with the best chance of winning the race.
Mathematics expresses itself everywhere, in almost every face of life - in nature all around us, and in the technologies in our hands. Mathematics is the language of science and engineering - describing our understanding of all that we observe.Mathematics has been around since the beginnings of time and it most probably began with counting. Many, if not all puzzles and games require mathematical logic and deduction. This section uses the fun and excitement of various popular games and puzzles, and the exhilaration of solving them, to attract and engage the students to realise the mathematics in fun and games.
Descriptive Statement
Number sense is defined as an intuitive feel for numbers and a common sense approach to using them. It is a comfort with what numbers represent, coming from investigating their characteristics and using them in diverse situations, and how best they can be used to describe a particular situation. Number sense is an attribute of all successful users of mathematics. Our students often do not connect what is happening in their mathematics classrooms with their daily lives. It is essential that the mathematics curriculum build on the sense of number that students bring with them to school. Problems and numbers which arise in the context of the students world are more meaningful to students than traditional textbook exercises and help them develop their sense of how numbers and operations are used. Frequent use of estimation and mental computation are also important ingredients in the development of number sense, as are regular opportunities for student communication. Discussion of their own invented strategies for problem solutions helps students strengthen their intuitive understanding of numbers and the relationships between numbers.
In summary, the commitment to develop number sense requires a dramatic shift in the way students learn mathematics.
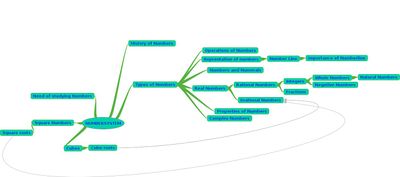
Mind Map
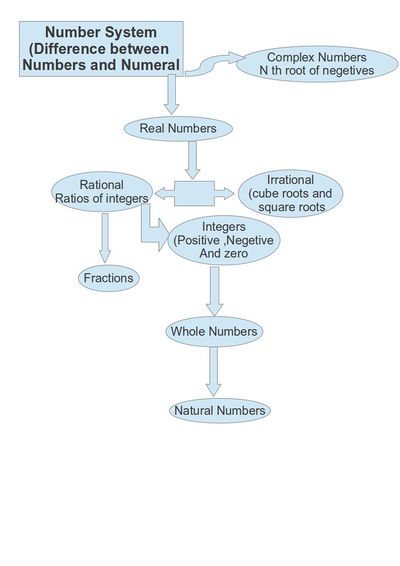
Flow Chart
What are numbers - A Bridge course in Class 8
This unit on number systems is in three parts. The first part will be to develop in children a sense of numbers, the idea of quantity, counting and mathematical manipulation, collections of quantities and developing a unit of measure. The second would be to develop the ideas of the negative numbers and build an understanding based on the manipulations of numbers. The third part would be to introduce the number line as a continuum and to introduce ideas of fractions and rational numbers.While this is for classes 7and 8, we understand that students may come with very limited sense of the numbers. So the activities are designed in such a way as to help such students also.
Part I: Number Sense – Counting and Operations
Objectives
1. Understand that there is an aspect of quantity that we can develop with disparate objects
2. Comparison and mapping of quanties (more or less or equal)
3. Representation of quantity by numbers and learning the abstraction that “2 represents quantity 2 of a given thing”
4. Numbers also have an ordinal value – that of ordering and that is different from the representation aspect of numbers
5. Expression of quantities and manipulation of quantities (operations) symbolically
6. Recognizing the quantity represented by numerals and discovering how one number is related to another number
7. This number representation is continuous.
Lesson 1 : Quantity and Numbers
Teacher Note - this is not one period – but a lesson topic. There could be a few more lessons in this section. For example, for representing collections and making a distinction between 1 apple and a dozen apples. This idea could be explained later to develop fractions. Another activity that can also be used to talk of units of measure. Addition and subtraction have been discussed here – extend this to include multiplication and division).
Objectives of the activity
- To develop an understanding that quantity is something we associate with objects and there are different ways of representing this and that different objects have different measures of quantity
- Represent quantity as numbers and express symbolically
- Understand the difference between the ordinal value of a number and the representation of a quantity
- Manipulate numbers, perform mathematical operations and express these operations symbolically in mathematical language.
- Apples in two groups (or any other fruit)
- Small cards for writing down the numbers as well as for writing the operations
- Pencils, etc
- A collection of other objects – stones, sticks, notebooks
How to do the activity
- This whole activity can be done in groups with different sets of objects
- Keep two group of apples separately.
- Keep them in physically different arrangements.
- Based on visual inspection and counting, determine the number of apples and which group is larger or smaller or if both are equal.
Questions for discussion:
- How can you describe the two groups? [ Words – red, large, small, more, less]
- Which words are being used first – more or less, dozen, kilo
- What is the first thing you want to do when you see the two groups?
- The students may start counting – but ask them for other ways of understanding the quantity (trying to do a one-to-one correspondence between the two groups of apples)
- If for every apple in one group, I have one apple in the other group, then I do not need to count at all. Can this one to one be done with anything other than apples? [ children, ribbons, stones]. This can bring about the idea that quantity is something that is present in many different objects
- With this mapping can I say more or less or equal? Now represent this by numbers; and discuss the difference between the two comments below: “There are 6 apples in group 1” and “This is the 6th apple in the first group”.
- Can these numbers represent only apples or anything else? Does this number “2” mean the same thing when I am counting dogs or notebooks?
- Manipulating the quantities. By physically combining and representing them in numbers, introduce the idea of mathematical operations of addition and subtraction
Part 1
- Bring the two groups of apples together. Add Group 1 to Group 2. Describe what happens [ Words – more, large, big, add]
- What did this process do? I had two groups and I mixed them? What happened?
- Can I mix them like this all the time? Why? Why not?
- If I have apples and notebooks can I mix them? Why? Why not?
- Introduce the idea of “+”. This process is called addition and is represented like this.
- Let us separate the two again. And count the number in each group. Add Group 2 to Group 1. Does it matter? Are the results the same?
This can be written as 5 + 6 = 11
The “+” is called a mathematical operator. The addition is called an operation. These operations have some properties and they always hold.
Separate the two groups again. Can I add only all of them together? Or can I add 1 at a time, 2 at a time, 3 at a time?
The ideas to be introduced would be Skip counting and quantity increase is continuous.
addition worksheet
Part 2
- Now from the large group take away some apples. What happens to the number? What have we done?
- We have reduced the large group by 3 apples. This can be written as 11 – 3 =8. When I mixed two groups what did we do? And what are we doing when we are separating the two groups? This will introduce words like increase, decrease, subtract, opposite.
- Pose this question like this – “ I added 5 apples to six apples to make it 11 apples. What should I do to a bag of 11 apples to make it have 6 apples again”. I take away 5. This is called subtraction and is the inverse process of addition.
The “-” is called a mathematical operator. The subtraction is called an operation. These operations have some properties and they always hold. subtraction worksheet
Evaluation activities
- Create situations where children work in groups and compare collections of items without counting.
- Have groups work with 3 groups of fruits, sticks, pencils, etc. The idea that addition can be extended indefinitely can be discussed.
- Subtraction with quantities without getting into negative numbers.
- Children must orally and in a written form represent these operations.
- Create different sets of objects and ask the children to add [ to test for the legitimacy of addition]
- Adding to quantity in 2's, 3's - Combinations of 2 numbers that will give 10 as an answer. Can you guess the pattern for combinations of numbers that will give 20 as an answer? [ Subtraction is an inverse process of addition]
- In their community, street, what is their house number? What does this number mean?
- How will you count mustard, sand, apples and sugar? The children will discuss this in groups and discuss with the class
- Worksheets of simple problem solving – with just number manipulations
- Worksheets of simple problem solving – with word descriptions. Children can either draw these answers or write them in statements. Evaluate the ability of the child to process written instructions.
- Worksheet: Number Stories
Part II – Negative Numbers
Objectives
- To extend the understanding and skill of representing symbolically numbers and manipulating them.
- To understand that negative numbers are numbers that are created to explain situations in such a way that mathematical operations hold
- Negative numbers are opposite of positive numbers; the rules of working with negative numbers are opposite to that of working with positive numbers
- Together, the negative numbers and positive numbers form one continuous number line
- Perform manipulations with negative numbers and express symbolically situations involving negative numbers
Lesson 1 : The idea of negative numbers and operations on negative numbers
Objectives of the activity
- Develop an idea that negative numbers are part of a type of numbers
- That negative numbers are continuous
- Repesent the number line with zero as a place holder
Materials needed
- More apples (or any other fruit)
- Small cards for writing down the numbers as well as for writing the operations
- Pencils, etc
- Two boxes – one of negative numbers and the other of positive numbers
How to do the activity
Part 1
1. By the previous activity we have 11 apples. Now we add a few more. Let us say we add 4 more. We have 15 apples.
11 + 2 = 13 + 2 signifies increase in apples 13 + 2 = 15 Write the expression. Again + signifies increase
2. Let us say I ask the question – what should I add to 15 to make the number of apples 10?
They will say ”take away”. Let us say we cannot use the word “take away”.
Write the expression like this 15 + (-5) = 10.
3. The numbers that when added to a number increase the original quantity are called positive numbers. The numbers that when added to a number decrease the original quantity are called negative numbers. The negative number is thus an opposite of the positive number.
4. Now frame the question as follows
- What do I have to add to 15 to make it 7? The answer is (-8).
- What do I add to 15 to get 8? (-7)
- What do I add to 15 to get 9? (-6)
- What do I add to 15 to get 10? (-5)
When I add (-7). I get 8. For me to get 9, I have to add a number greater than (-7) and I have added (-6). Similarly (-5) is greater than (-6). So the larger negative number is actually smaller.
6. Now we transition from numbers representing some quantities to numbers being manipulated as numbers.
Part 2
1. We have seen what negative numbers are. We will see how to work with them.
2. We have seen that negative numbers are such that when we add them the quantity decreases. What happens when we subtract them?
3. Extend the activity of what should I add to 20 to make it 10, 11, 12 and so on? Extend it all the way to 30. Let the students pull the numbers out and place them along the wall/ stock on the wall etc. You will see the number line.
4. Let us pull out sets of numbers the same number but from the positive box and negative box.
3, -3
Add them
3 + (-3) = 0
4, -4
Add them
4 + (-4) = 0
This addition could be explained like this. When I add three the quantity increases. When I add -3 the quantity decreases. So + 3 and -3 are the same in magnitude but do opposite things. For every positive integer, there is a negative integer. Discuss examples of borrowing from the bank; someone giving a loan.
5. Now I have 25 (from the number box). I am going to subtract (-5). What will happen? When I add (-5), it becomes 20. Since negative numbers behave in this opposite way, subtracting (-5) should become 30? 25 - (-5) = 30...this is equivalent to adding 5 to 25. Hence we say (-)*(-) = +
Now what happens when we multiply negative numbers?
- Let us take -3 x 3. From the process of multiplication is repeated addition we can explain as take -3 once, take it the second time and third time. We have -3, -3, -3. We have -9.
- 3 x -3 . Again multiplication is the process of repeated addition. Except I am multiplying it by -3. Then I have to look at the operation as opposite. I am giving away 3 once, twice and third time. We have -9.
- -3 x -3. How do we do this?
Let us look at the table below.
- 3 x 3 = -9
- 3 x 2 = -6
- 3 x 1 = -3
- 3 x 0 = 0
- 3 x-1 = -3
- 3 x-2 = -6
- 3 x-3 = -9
Extend the pattern above. By simple pattern evaluation we see it is 3, 6 and 9. We have shown the number line above. It makes sense logically that the next number is 3 and that it becomes positive. The best way to extend this to division is to treat this as multiplication by fraction and extend these rules.
Yet another way of explaining could be like this. When we add -3, -3 times we are actually operating with two opposites. The (-3) times signifies the opposite of the repeated addition, think of it as repeated subtraction. I am subtracting -3 once (in effect, adding 3); -(-3) second time (adding another 3) and -(-3) for the third time -(-3) (adding one more 3). We get 9. Hence -(-) is positive.
Evaluation activities
- Start doing this activity with objects, then numbers depending upon the level of the student.
- 6 - 1? - what is the answer?
- 6 - 2? - what is the answer?
- Continue this exercise until we get to
6 - 7? Can we take away the objects? We start looking at these as a special kind of number and get the number line to move to -1. Extend the number line construction. What does this – 7 represent (they should say it means that when I add this it is reducing the quantity)
- Arrange a set of randomly chosen positive and negative numbers (integers) along the number line in increasing order.
Part III: The number line in mathematics
The number line is not just a school object. It is as much a mathematical idea as functions.
The number line is a geometric “model” of all numbers -- including 0 1, 2, 25, 374 trillion, and -5, Unlike counters, which model only counters, the number line models measurement, which is why it must start with zero. (When we count, the first object we touch is called "one." When we measur using a ruler, we line one end of the object we’re measuring against the zero mark on the ruler.

Part of the power of addition and subtraction is that these operations work with both counting and measuring. Therefore, to understand basic operations like addition and subtraction, we need a number line model as well as counters.
The number line in teaching mathematics
One reason to use this mathematical object with students is that they need to see arithmetic in both contexts: counting and measuring. At the beginning, children may sometimes use the number line to find answers to arithmetic problems (e.g., figuring out what 3 + 10 is, before that becomes automatic to them) but that is never its purpose. We don’t rely on the number line for getting answers -- for that, we want the children to know basic facts and methods and use their heads -- but we do use the number line to understand things about the operation (addition and subtraction) and to understand what the answers mean.
For example, the answer to the subtraction problem 92 – 49 is the distance between those two numbers on the number line. That image can greatly help mental computation: 49 to 50 is one step, 50 to 90 is another forty steps, and 90 to 92 is another two steps, so altogether 43 steps. (See number line addition and subtraction below.) It also makes arithmetic with negetive numbers which has been already discussed. And the number line is essential for full understanding of fractions and decimals. In fact, a ruler (a number line!) is one of the important places students encounter and need to use fractions.
In counting
Number lines are first used just to show sequence—numbers standing on line in order! At this stage, neither the straightness of the line nor the distance between numbers is mathematically important, though our images are always standard anyway. Children will look at chunks of the line, not always starting at 1, and will work forwards or backwards from some number that is placed on the line. They are learning about sequence and order, and that develops somewhat independently from counting.
In measurement

Students also learn about intervals on the number line, but just begin that process. Kids used to gain the interval idea (in a slightly different form) from their experience playing board games. They knew that when they rolled a 5, they had to count their five spaces beginning with the next space. That is, they were counting moves, not positions. Measurement depends on it. Addition and subtraction with counters does not depend on it, but those operations on the number line do depend on it.
In addition and subtraction
If we can add and subtract with counters, why use the number line? To connect these operations with measurement, and also because the counters no longer suffice when we get to fractions, decimals, and negative numbers. Over time, kids will connect number line images with thermometers, clocks, rulers (with fractional inches)… Coordinate graphs are based on perpendicular number lines; even bar graphs require the measurement idea more than the count idea, although they can begin with count. Addition and subtraction, or comparison, of distance is also why we use number lines. Adding distance is further developed on open number lines. Students develop many ways to subtract (in second grade, they learn to subtract 8 from anything by subtracting 10 and then compensating, and then they extend that idea to other additions and subtractions).
Hopping on the Number Line
In this lesson, students generate sums using the number line model. This model highlights the measurement aspect of addition and is a distinctly different representation of the operation from the model presented in the previous discussion. The order (commutative) property is also introduced. At the end of the lesson, students are encouraged to predict sums and to answer puzzles involving addition.
Activity 1 - To introduce Number line
Objectives
- Represent the number line using objects.
- Count each group of ones objects.
- Relate the cumulative total of each group to the number on the number line. Write the cumulative total for each group.
- Skip count by pointing to each group of objects.
How to do the activity
Encouraging students to come to the number line and skip count by ones pointing to the numbers on the number line that represent each one.
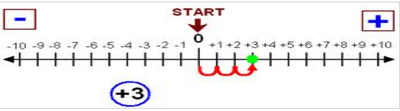
Discuss a sample problem like this. Ram and his dad are driving to the city. It is 15 kms away. They have already gone 5 kms. How many more kms do they have to drive?
After a minute or so, ask for a few children to share with the class.
You have to figure out how much farther they have to drive. You could keep going, like count up from 5 to 15. You could go maybe go backwards from 15 down to 5. Students will probably have a variety of ideas for solving the problem, including counting on from, or adding to 5 to reach 15, or counting backwards from 15 to find out how many kms remain.
Summarize both approaches by writing the following equations below:
5 + □ = 15
15 – □ = 5
Discussion
We could say we just keep going from 5 up to 15, so we wrote 5 + box equals 15. What does the box mean in this equation? The students may say it means part you have to figure out. It’s where you write the answer. It’s like the problem you have to solve. 5 plus how many more to get to 15?
Another interpretation is that it is like you’re finding out how far you have to go backwards to get down to 5. This is the idea that subtraction is the inverse process of addition.
After taking students’ ideas, it is possible to introduce number lines as a new tool for solving problems like these. Number line can be drawn as a horizontal line across the board. Include an arrow on either end to show that the number line continues indefinitely in both directions. Record the smaller number (5) by marking and labeling a dot on the far left side. Then propose to move along the number line by hops greater than 1 to find the difference between 5 and 15.
This discussion can be extended with the following question. What if Ram and his dad drive 2 more kms? How far will they be then? This can also be shown on the number line. What if they drove 3 more kms after that? How far would they be? The students should be able to say they are upto 10 miles!
They have gone 5 miles after the 5 because 2+3=5 and it is possible to know how many more miles they have to go to get to 15!
Ask students to suggest additional hops you could take along the number line to get to 15.
You could keep going by ones, like 1 and then 2and so on more little hop up to 15.

And this can be generalized for negative numbers also.
Evaluation Questions
- How much farther did Ram and his dad have to drive to get to the city?
- How do you know? Can you show us on the open number line?
- Does this give us the answer to the problem?
- Did we add or subtract to find the answer?
Worksheet for hopping of numbers
- click here for level one, concept of hopping on number line.
- click here for level 2 worksheet on hopping on the number line.
Activity2 - Sum and product of numbers
Objectives
- Using the number line model to find sum and products
- Solving and creating puzzles using the number line
- Investigating the order property of addition and multiplication
Materials
Counters for the number line (chips, markers, etc.)
How to do the activity(addition)
Tell the students that they will find sums using the number line model. Then display a large number line and a 5+4 pencils , that is, a pencil with 5 spots on the left side and 4 spots on the right. Then demonstrate with a counter how a hop of 5 is taken on the number line. You may wish to encourage students to count aloud as the hop is made. Then make a hop of 4, starting at the place the counter landed. You might choose to have them record what happened using the equation notation 5 + 4 = 9, or to informally describe the moves this way: “If you take a hop of 5 spaces and then a hop of 4 spaces, you land on 9.” You may wish to highlight the fact that in this model, spaces are counted, not points on the number line.
Questions for discussion
- Which number did you land on when you made a 5-hop, then a 3-hop? Could you land on the same number if you took a 3-hop first, then a 5-hop? How do you know?
The answers could be yes [ 5 + 3 = 8, and 3 + 5 = 8.]. Laws of computation can be introduced.
- What sums did you model with hops? How did you record them? [Student responses will depend upon the "hops" they performed.]
- Were any of the sums the same? Why? [Student responses will depend upon the "hops" they performed.]
- How would you find the sum of 2 and 5? [Make a hop of 2, and then a hop of 5, to reach 7.]
- How would you tell a friend to add on the number line?
- How is using a number line like measuring? How is it different?
- Which students counted as they took hops and which moved directly to the number?
Questions for teacher reflection
- Which students had trouble using the number line? What instructional experiences do they need next?
- Did any children notice a connection with measurement?
- What adjustments would we make the next time that we teach this lesson?
Activity using GEOGEBRA
Addition using number line can be demonstrated using Geogebra.
See image below
Click here for an animation.
Click here to download the Geogebra file.
Bridge course Resource
Topic:Number system
Activity : Understanding numbers, properties through number line
Time duration: 60 minutes
Materials required: paper ,pencils/sketch pens
Objectives:
1. Understanding what is a number line
2. Understanding properties(behaviour) of positive and negative numbers through number line
3. Understanding number sentences /operations of numbers on the basis properties of numbers.
4. Compare numbers/ordering numbers
Pre-requisites:
Students know about numbers,Numbers are continuous, counting, quantities for ex: difference between 2 books,2 kgs of apples or 2 litres of milk,2 mts .....
Note for the teachers :
Please emphasise that positive numbers increase the quantities and negative numbers decreases the quantity(amount)
Procedure:

Step 1
Ask boys to write positive number and girls to write negative numbers on a sheet of paper. Each one should write one number. Instruct them to arrange the numbers in order on the floor.
Now ask boy and girl to come one after other to keep the number which they have written .
Suppose the first boy comes and keeps +5 then call other girl ask her to keep her number .
She can keep it anywhere she wants (imagine she has -7 on her sheet)
But the real fun starts when the third one(boy) will come(imagine he has +10 on his sheet)
You have to help him to keep the number in a proper order as he will have a positive number you should guide him where he should keep it and why?
+5
-7
If the numbers are kept as above where +10 should be placed?why?
For this we need to explain +5 has property of increasing the quantity by 5
whereas -7 has a property of decreasing the quantity by -7,(+5 is more than -7) so where should be place for +10
.
+10 has a nature of increasing the quantity more than what +5 does .so keep it above +5.
(+10 is more than +5)
+10
+5
-7
If the next girl comes with -4 ,where she should keep it?
Repeat the developmental questions like
What is the behaviour of -7 and -4
(-7 decrease the quantity by 7 where as -4 decrease any quantity just by 4)
Try to extract from them that -4 is more than -7.
Continued pattern will be
+10
+5
-4
-7
Place all the numbers what they have written on the sheet.
Step:2
Ask them
Is there any number missed in between?
If the answer is yes ask them again to write the missed numbers and repeat the activity by placing those numbers in a right place, which completes the number line. Now explain number line is a model for representing numbers .
Now the number pattern will look like this after filling the gaps
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
+1
+2
+3
+4
+5
+6
+7
+8
+9 (You can also ask which is the last number?) The number arrangement need not be horizontal
Step:3
Now write some number sentences as below .Help them to interpret the sentences.
4+(+3)=+7
The value of 4 increased to +7 when it is added to +3 (+3 increases the value of 4 by how much?)
4+(-3)=+1
The value of 4 decreased to +1when it is added to -3 (-3 decreases the value of 4 by how much?)
-4+(+3)=-1
The value of -4 increased to +7 when it is added to +3 (+3 increases the value of 4 by how much?)
-4+(-3)=-7
Help them to interpret the above sentences.
Give some examples to verify the resuts like
-4+(-3)=-1
Do they able to check value of -4 should decrease by 3.But resultant value -1 is greater than -4
So this is a wrong statement.Askthem to correct it.
Prepare worksheets for practise.
How to do the activity - Multiplication
On the overhead projector or chalkboard, display a large number line and demonstrate with a counter how hops of 5 can be taken on the number line. You may wish to encourage students to count aloud as the hops are made. You might choose to introduce the equation notation 4 × 5 = 20, informally reading it as "Four hops of 5, and you land on 20." After several examples with 5 as a factor, ask the students to determine what size hop to use next. Encourage the students to predict the products and to verify their predictions by moving a counter on the large numberline. You may wish to provide children with a counter and individual number lines at their desks.
After allowing time of exploration, ask the students to predict the answers to questions such as "If I take 4 hops of 3, where will I land?"
Now give each student a piece of paper and ask them to make up 2 similar problems and trade them with a friend to solve using the number line. When the pairs have finished, call them together to discuss what they did. Encourage them to use the number line in their explanation.
Be sure students have the opportunity to explore different factors, such as:
2 × 3
4 × 4
3 × 6
7 × 2
and so on....
Then ask: "If I take 5 hops of 3, where will I land? How about if I take 3 hops of 5? Will this work every time?" Encourage them to explore the order property and state their findings. [In each case, the student should land on 15, because of the commutative property of mulitplication.]
As a concluding activity, you may wish to pose puzzles such as "I am a number between 20 and 30. You say my name when you hop by 5's. Who am I?" and encourage students to create and share similar problems.
Questions for StudentsWhat numbers did you land on when you hopped by 5?
[5, 10, 15, 20, etc.]
What numbers did you land on when you hopped by 3?
[3, 6, 9, 12, 15, etc.]
Assessment
At this stage of the unit it is important for students to know how to:
use the number line model to find products
the order property of multiplication
solve and create puzzles using the number line
The guiding questions suggest ways to help you determine if students have achieved these objectives. You may want to add others that the conversations with the students suggest. The notes recording sheet provides a form on which to document your observations about student understanding and skills. You may find this information useful when discussing progress toward learning targets with individual students.
Sub Theme:Fractions Introduction: Fractions are defined in relation to a whole—or unit amount—by dividing the whole into equal parts. The notion of dividing into equal parts may seem simple, but it can be problematic. Although we use pairs of numbers to represent fractions, a fraction stands for a single number, and as such, has a location on the number line. Number lines provide an excellent way to represent improper fractions, which represent an amount that is more than the related whole. Instruction in fractions that focuses only on the mechanics of procedures and not on reasoning misses valuable opportunities to guide students in developing this core mathematical skill. This section explains the meaning of fractions, reviews some of the common difficulties in understanding the meaning of fractions, and describes how to use simple pictures to represent fractions.Fractions arise naturally whenever we want to consider one or more parts of an object or quantity that is divided into pieces. Consider how fractions are used in the following ordinary situations:
In this section, we define what we mean by a fraction is part of of an object, collection or quantity.
The five meanings listed below serve as conceptual models or tools for thinking about and working with fractions and serve as a framework for designing teaching activities that engage students in sense making as they construct knowledge about fractions.
1.Part of a whole 2.Part of a group/set 3.Measure (name for point on number line) 4.Ratio 5.Indicated divisionInterpreting fractions
Given their different representations, and the way they sometimes refer to a number and sometimes an operation, it is important to be able to discuss fractions in the many ways they appear. A multiple representation activity, including different numerical and visual representations, is one way of doing this. Sharing food is a good way to introduce various concepts aboput fractions. For example, using a chocolate bar and dividing it into pieces. This can be highly motivating if learners can eat it afterwards. A clock face shows clearly what halves and quarters look like, and can be extended to other fractions with discussion about why some are easier to show than others. We can find a third of an hour, but what about a fifth?
A paper tape measure is a valuable illustration of
different fractions. For example, learners can write on 1/2m, 0.50m and
50cm for their own portable equivalence chart.
Folding of paper also can illustrate fractions
I have ten bars of chocolate, and I share them equally between four people. How much will they each get?
We recommend that teachers explicitly use thelanguage of fractions in other
parts of the curriculum for reinforcement. For example, when looking at
shapes, talk about ‘half a square’ and ‘third of a circle’.
Activity
What represents the whole? Materials needed paper pencils scale How to do the activity? Try this activity using these Pattern Block pieces:
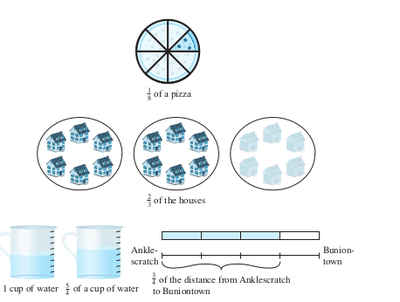
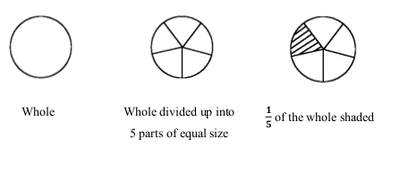
This activity helps to show that, for example, the green triangle Pattern Block could represent one whole, one ,half, one third, or one sixth, depending on what we select to represent the whole. At this point I would hasten to observe that the same could have been said for the 1/4 circle, but since its almost impossible to get anyone to see beyond the "obvious whole" that the circle represents, we need to rely on other shapes to deliver that message. Fractions and wholes: introductory concepts and activities Fractions can be used to represent numbers which are not whole numbers. As such, they are slightly more difficult to come to terms with than whole numbers. The first two sections of this unit will look in a detailed manner at sound methods for the teaching of fractions to young learners. You should be able to follow these ideas and ensure that all of this information given is part of your own knowledge. It is vital that all teachers of mathematics have a good concept of fractions themselves. We need to ensure that the learners are given adequate exposure to a great enough variety of examples of fractions in concrete demonstrations, so that they are able to form their own abstract concept of what number the fraction numeral represents. So we will begin by looking at fractions as parts of concrete wholes and progress from there to more abstract working with fractions. The first important thing we should stress is that we can find fractions of continuous and discontinuous wholes. These two types of wholes are not always given equal representation. We should not emphasise one more than the other or we risk giving an unbalanced idea of concrete wholes. Summary A continuous whole is a single item which is cut/folded/broken/divided up into parts of equal size in one way or another in order to find its fraction parts. Examples of continuous wholes are: an orange, a piece of paper, a slab of chocolate, a circular disc, a loaf of bread etc. A discontinuous whole is a group of items that together make up the whole. To find a fraction part of such a whole, we can divide it up into groups, each with the same number of items. We call such groups "equal-sized groups" or "groups of equal size". It is important that we always mention thathe groups are equal in size to emphasise this aspect of the fraction parts of a whole. Examples of discontinuous wholes are: 15 oranges, 6 biscuits, 27 counters, 4 new pencils, etc. Language patterns for a continuous whole To find 1/5 of my circular disc, I first divide the whole circular disc into 5 parts of equal size. Each part is 1/5 of the whole, and if I shade one of these parts, I have shaded of the 1/5 whole.
Activity
Activity through worksheet
Activity Activity through worksheet
Until now we have only found fraction parts where the denominators relate to the number of units in the discontinuous wholes. Now we look at a slightly more complex form of discontinuous wholes. Examine the following examples. Notice that the first examples relate to unit fractions, while the later examples relate to non-unit fractions.
Activity Activity through worksheet
concrete wholes and numeric algorithms. As we progressed through this unit, we used different types of wholes, though we just referred to them as different types of continuous and discontinuous wholes. We can name these different types of wholes according to several categories. You need to know these categories and be sure to expose your learners to all of them, in a logical sequence of ever-increasing difficulty. The categories are listed in order of complexity. The examples are all left for you to solve, as a revision of work we have already done.
Categories of the whole – a review of concepts In the first three sections of this unit we looked at finding fractions of different wholes and there we found equivalent fractions and compared different fractions using both Activity Activity through worksheet
Concrete wholes and numeric algorithms. As we progressed through this unit, we used different types of wholes, though we just referred to them as different types of continuous and discontinuous wholes. We can name these different types of wholes according to several categories. You need to know these categories and be sure to expose your learners to all of them, in a logical sequence of ever-increasing difficulty. The categories are listed in order of complexity. The examples are all left for you to solve, as a revision of work we have already done.
Category 1: Continuous The unit whole. All wholes which consist of a single item fall into this category. To find a fraction part of a unit whole, we have to cut/fold/break, etc. because the whole is a single thing.
Category 2: Discontinuous (made of more than one item) The whole consists of more than one unit, but the number of units is limited to the same number as the denominator. It is thus made up of more that one item and is a discontinuous whole.
Category 3: Discontinuous (made of more than one item) The whole consists of more that one unit, but the whole is always a multiple of the denominator. This is also made up of more than one unit and so it is a discontinuous whole.
Category 4: Discontinuous (made of more than one item) The whole consists of more than one unit, but less than the number of units in the denominator. This is also a multiple unit whole, and so it is a discontinuous whole.
Category 5: Discontinuous (made of more than one item)
The whole consists of more than one unit, and more than the number in the
denominator. This is another discontinuous whole.
The ability to place a fraction on a number line follows from having a part-whole understanding of fractions, and being able to compare and order fractions. For some students using a number line can help them visualise the size of a fraction, and can provide them with a tool for representing and comparing fractions.
Context The number line relates to the context of distance and length and questions like "how far along.?" can access student's prior understandings. This context is already a part of student experience. It can also be introduced using the context of a milk bottle, by asking how full is (a given mark) and using common fractional amounts used in conversation (i.e., a quarter, half, third, etc).
There are two distinct types of resource about fractions and number lines: Writing or ordering fractions in pre positioned boxes along number line. This can illustrate how a number line can be used to represent fractions of distance or length; or support the notion of a fraction being larger or smaller than another. Marking the fraction on an empty number line - this involves measurement and judgement of a fraction as a proportion of a length or distance.
Activity to represent fraction on Number Line
Show where 1/2, 2/3 and 3/4 would be on the number line below.
Materials Black board chalk
How to do the Activity
Writing or ordering fractions in pre positioned boxes along number line. This can illustrate how a number line can be used to represent fractions of distance or length; or support the notion of a fraction being larger or smaller than another.
For example: Write the fractions that would go in the boxes below.
Fraction is a number that describes part of a whole number. Because fractions are numbers just like 5, or 2, or 23, they live on a number line. A fraction is made up of a numerator and a denominator: numerator/denominator The denominator tells how many parts each unit interval has been cut into. The numerator tells how many of those parts you have. For example, in the fraction 85 the denominator 8 means each unit interval has been cut into 8 parts. The numerator 5 means you want to start at 0 and move to the right five parts.
Similarly, the fraction 811 means each whole step has been cut into 8 parts and you want to move to the right 11 parts.
This picture is also a visual representation that 811 is equal to 183.
To identify where 49 lives on a number line, you need to recognize that each whole unit has been cut into 4 parts and you need to move to the right nine parts.
This is a good way to show that 49 is equal to 241.
Where is point Q located on the number line?
First count the number of parts the distance from 0 to 1 has been cut into: 8 parts
Secondly, count the number of parts Q is to the right of 0: 6 parts.
So, Q is located at 86.
Where is point Q located on the number line?
There are two ways to think of where Q is on the number line.
The red arcs show that Q is located at 15/2. The green arc shows that Q is located at 5/7. Sub theme:Decimals Introduction
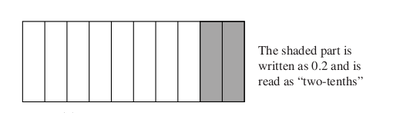
Decimals are a way of representing fractions or parts of a whole. This unit has been prepared to extend the knowledge and skills you gained in Units 1, 2, and 3 on fractions. Decimals are yet another way of representing numbers. You will be exposed to ways of enabling your pupils understanding of base 10, place-value and fraction concepts and clarifying these ideas encountered in out-of-school activities. In many real life situations, people read scales, measure lengths, weigh objects, and deal in money, all areas where decimals are met. These will form focal points for learning decimals in this unit. Objectives After working through this unit you should be able to: • represent and use decimal fractions in a variety of equivalent forms in real life and mathematical situations • develop number sense for decimal fractions in your pupils • enable your pupils to carry out calculations with decimals using the four operations Introducing Decimals When you were taught decimals, you were probably introduced to them by changing common fractions, and then by the direct division method. This approach works well, if fractions were grasped by pupils. It has been shown through research (Cockcroft 1982) that many pupils have problems in understanding the meaning of two or more decimals places, i.e., hundreds, thousands, etc. Unit Activity 1 1. Construct five tasks to test pupils’ understanding of decimals. 2. Interview at least four pupils on the task above. 3. Discuss with a colleague what you observed and learned from the outcome of these tasks and the interviews. 4. How do you think decimals should be introduced? Before you go on, read the next few pages and write down ideas of your own. Model for Introducing Decimals Proportional model – tenths Pupils should form concepts of decimals and learn the meaning of each place in a decimal. Introduce a decimal first as a fractional part of a unit. For this idea, you need a diagram, like Figure 3.1 below, with 10 equal parts.
The shaded part is written as 0.2 and is read as “two-tenths”
Ask students to shade 1/10, 4/10, 5 /10 , , , etc. State that there are two ways of representing the ’shaded’ or coloured areas. Pupils will be familiar at this stage with the common-fractions form. Introduce the decimal notation form. This should be modelled by how it is written. Ask students to shade or colour fractions such as e.g. .1, .4, .6 At this stage two peculiarities of decimal notation should be mentioned. First, for numbers less than 1, the decimal is written as 0.1 or 0.4 or 0.6 etc. (not just as .1) and is read as one-tenth, four-tenths, six-tenths, etc. Secondly, whole numbers are sometimes recorded using a decimal point, e.g., 4.0, 6.0, 82.0 indicating that they are whole numbers with no tenths. Practice Activity 1 Find objects or figures with ten equal parts or better still improvise by drawing on card-board boxes grids you can cut out. 1. Ask pupils to colour two-tenths, seven-tenths, three-tenths, nine-tenths, etc. 2. Ask pupils to write these parts as decimals. 3. Write different decimals (tenths), and ask pupils to read them out aloud, one at a time. Ensure that pupils know that 10-tenths is the equivalent of a whole (1) and that 17-tenths is more than a whole. These ideas should have been developed when pupils dealt with fractions. Mixed numbers involving whole numbers and decimal parts are written and read as follows: 2.4 is commonly read as ‘two point four’ but should be ‘two and four tenths’. Delay the use of ‘point’, as in ‘two point four’, because this brings out the meaning of the place 4 holds (four-tenths). Give pupils maximum opportunity to practice reading decimal numbers (e.g., read 5.6 as five and six-tenths). Make simple translations between fractions and decimals notations. For example, ask pupils to calibrate a number line in tenths.
Develop concepts of which is bigger, e.g., between 0.9 or 1.2 by posing several questions. If this is related to fractions, pupils should be able to grasp this easily. At this stage you may want to relate this to place value ideas, or you may have already done so. For easy explanation, we have deliberately separated the two This way we explain can decimals in terms of place value, and assuming your pupils have had enough practice, we can explain on to hundredths.
Conclusion and cotinuation to Rational Numbers
Fraction concept is a part of number concept, since fractions are the numerals (symbols)
for a group of numbers. But a fraction is no simple group of numbers.
Fractions can be used to express all rational numbers. This was discussed in Unit 2 of this
course. Rational number concept involves an understanding of fractions which involves
more than just the finding of parts of a whole. Learners need to be exposed to a range of
activities and conceptual teaching on fractions as parts of wholes, ratios, decimals and
percentages in order to develop fully their understanding of multiplicative reasoning and
rational numbers.
Fraction numerals are written as a numerator over a denominator. In your numeration
course we discussed the difference between a number and a numeral.
Do you remember the difference between a number and a numeral?
Reflection How does this difference start to speak to you about the difference
between knowing how to write a fraction numeral and knowing the
numeric value of that numeral?
Sub theme: Rational Numbers Introduction The words ‘rational’ and ‘irrational’ with regard to number in Mathematics has very little to do with the meaning of the English word. A rational number is part of a whole expressed as a fraction, decimal or a percentage. A number is rational if we can write it as a fraction where the top number of the fraction and bottom number are both whole numbers. In fact, they are the numbers that we use in every day life. The term rational is derived from the word ratio because the rational numbers are the ones that can be written in the ratio form. Every whole number, including negative numbers and zero, is a rational number. This is because every whole number ‘n’ can be written in the form n/1 (a fraction). For example, 8 = 8/1 and therefore 8 is a rational number. Numbers such as 4/7, -3/5, are also rational because their numerators and denominators are both whole numbers. Also, all repeating decimals like .43434343…, all integers and all finite decimals such as .371 are rational. The Rationale of the Rationals When people began to get serious with numbers, they realized you needed something more than integers. After all, there were times when you had to deal with parts of a number. Eventually, then, someone - particularly the Babylonians and the Egyptians - developed the concept of fractions or more exactly, the rational numbers. Rational numbers are best represented as ratios of integers (the word rational refers to the ratios, not anyone's ability to reason). Integers are also rational numbers as they can be represented as ratios (0/1, 1/1, -1/1, 2/1, 3/1). But the other rational numbers fill the spaces in between the integers. For a while a lot of people (mostly the Greek philosophers) thought that the rational numbers were all the numbers you needed. And for the practical purposes of everyday problems, they were right. Even today computers use rational numbers in all their calculations, even when using formulas that involve irrational numbers like π and e. After all, any irrational number that is rounded off becomes a rational number, and if you want to measure the circumference of a circle, depending on how accurate you wanted to be, you can multiply the diameter by 3, 22/7, 355/113, or 314159265358979/100000000000000. But in trying to count the rational numbers, you encounter a property they have that is not shared by integers. Rational numbers are dense. That is, if you pick any two rational numbers, you can find another rational number between them. That also means that if you pick any two rational numbers, you can pack any number of other rational numbers between them. So it seems there has to be more rational numbers than integers. But that's what people thought abut the integers, too, and when George set out to count the rationals, he was not being irrational.
A Rational Arrangement
Like George's proof about the integers, you can find all sorts "diagrammatic demonstrations" that rational numbers are countably infinite. One such - quote - "proof" - unquote - is shown below. The idea is if you follow the arrows you'll find all the rationals you want, and there's always a matching counting number for every rational.
A - Quote - "Proof" - Unquote This diagram really doesn't prove the case, of course. For all we know the set of rational numbers grows faster than the counting numbers, and all we're doing is matching up only the first few elements of each set. What we need is a formula which will match every rational number to every counting number. If we can find such a formula, then the two sets must be the same size. But first, we'll begin at the beginning and decide exactly what rational numbers are - or rather how to best represent them. Rationals have two popular representations. One is as the ratios we showed above (1/2, 1/9, 4/33, etc.). The other notation is as a terminating or repeating series of digits (0.5, 0.111111..., 0.12121212...). On the other hand, for our purposes, the best way to represent rationals are as ordered pairs of the integers. Ordered pairs are simply two numbers in a particular order, usually represented in parentheses like, (1 , 2), (1 , 9) or (4 , 33). For these to be rationals, then, the first number is the numerator and the second is the denominator. The notation fits with the problem which is to find a function that takes an ordered pair, (i , j), and generates a unique counting number. f(i, j) = n where n = 1, 2, 3, ... and i and j are integers. This type of formula - with some restrictions - will establish the one-to-one correspondence we need. Now, as the psychiatrist said, we can begin, yes?
Some Definitions Definitions are commonly used in proofs.Kurt Godelin his famous theorem on undecidability devised a whopping 46 definitions where each successive definition was dependent upon the previous one. The purpose of definitions is they can simplify a proof although it may not seem like it in Kurt's theorem. But the nice thing about definitions is you really don't have to prove anything. A property of numbers from a definition follows immediately from the definition. In fact, in a lot of proofs the writer will say something like "And so our conclusion comes directly from our definition which as all but the most dense can readily see." However, for the sake of clarity we'll try to give a bit more elaboration - probably so much elaboration that we will insult the intelligence of all but the most dense. As the diagram above suggested, we need to come up with an arrangement of rationals that can be listed in a sequence. In doing so we will produce a proof in three parts: 1. First, as we said above, the rational numbers are defined as ordered pairs of zero and counting numbers. 0 = (0, 1) 1/2 = (1, 2) 3/4 = (3, 4) 1/32 = (1, 32) Here we note we have to exclude pairs like (1, 0) since 1/0 is not defined as a rational number (you can't divide by zero). That is, no ordered pair has the second digit as zero. Now we also need to address how distinct we want to be. That is, 1/2 is a rational number. But so are 2/4 and 50/100. The last two rationals have the same value as 1/2, yes. But should we treat these as different rationals? Because of the original definition of rationals - ratios of integers - we will treat such numbers as distinct as long as they have different integers. That is also in keeping with the original use of rational numbers and permits greater specificity in what they represent. For instance if you have a parcel of land and divide it into two sections and award one of those to Euripides for his bravery in the Peloponnesian War, then you have given him one half of the land. But suppose you have the father and son, Strepsiades and Pheidippides, who were both valiant in battle, but you don't have enough land to go around for another war hero. In that case, you divide the land into quarters and award one parcel each to Strepsiades and Pheidippides. So you have given two of the four sections to the family and now have one-half of the original land left over for someone else. So by our definition, 1/2 and 2/4 are different rational numbers, although they do have the same value. Oh, yes. Letting numbers like 1/2 and 2/4 be different rationals simplifies the proof.
A Point of Clarification At this point, some people remain unconvinced. After all, they say they can match the rationals 1/1, 2/1, 3/1, 4/1, with the counting numbers and have an infinite number of rationals left over. Therefore there must be more rationals than counting numbers. You can make the same argument for the number of integers being more than the counting numbers. You can match the positive integers, 1, 2, 3, ..., etc., with counting numbers and so have the negative integers (and zero) left over. So how can integers, rationals, and counting numbers be the same size? Not so fast, there, Pilgrim. Yes what you say is true, but completely irrelevant. When you say 1/1, 2/1, 3/1, 4/1, etc,. can be matched with counting numbers that is certainly the case - because 1/1, 2/1, 3/1, 4/1, etc. are indeed the counting numbers. So all you are saying is the counting numbers can be matched with the counting numbers. Or in other words, when you do your one-to-one correspondence, you are simply omitting to match up all the members of your set with the other set. On the other hand, if you want to say the set of rationals is not the same size as the counting numbers, you must prove that no function will give us a one-to-one correspondence to rationals and counting numbers. Only if you can prove no such pairing exists, then can you correctly claim the sets are not the same size. But what we just proven, both for the rational numbers and as we did earlier for the integers, that there are indeed such functions. So the sets of rationals, integers, and counting numbers must be the same size. Objectives Concept 1: The Various Meanings of Rational Numbers 1. Students learn how rational numbers fit in the number system. 2. Students experience part/whole, quotient, ratio/rate and operator relationships as the different interpretations of rational numbers. 3. Students recognize that rational numbers might be represented as percents and decimals, as well as in fractional form. 4. Students learn the language and notation for rational numbers. 5. Students order and compare rational numbers using number lines, rulers and symbols. 6. Students use part/whole representations, percents and decimals in context. Concept 2: Operating on Rational Numbers 7. Students estimate results of operations using models and benchmark numbers. 8. Students explore operations on fractions using conceptually-based models. 9. Students perform operations ( +, –, x, ÷ ) with rational numbers in fractional form. 10. Students use models to illustrate operations on fractions. Rational Numbers They include all numbers that "come to an end" or numbers that repeat and have a pattern. The rational numbers are those numbers which can be expressed as a ratio between two integers. For example, the fractions 1/3 and –1111/8 are both rational numbers. All the integers are included in the rational numbers, since any integer z can be written as the ratio z/1. All decimals which terminate rational numbers (since 8.27 can be written as 827/100.) Decimals which have a repeating pattern after some point are also rationals: for example, 0.083333333... = 1/12. The set of rational numbers is closed under all 4 basic operations, that is, given any two rational numbers, their sum, difference, product, and quotient is also a rational number (as long as we don't divide by 0.) Activity to introduce rational numbers Objectives
The student represents and uses rational numbers in a variety of equivalent forms.
The student is expected to generate equivalent forms of rational numbers including whole numbers, fractions, and decimals. Clarifying Activity with Assessment Connections The teacher prepares a jar of fifty marbles of different colors. Pairs of students draw a handful of marbles from the jar and record the numbers of each color and total number of marbles drawn. They return the marbles, pass the jar to the next pair, and then generate a variety of ratios that can describe the handful of marbles. Students then determine equivalent forms of the rational numbers that they generated. For example, a jar has 14 red, 28 yellow, and 8 white marbles. Students pull 18 marbles from the jar: 6 red, 9 yellow, and 3 white. They may describe their handful of marbles in the following way: The portion of the handful that was red is 6/18 = 3/9 = 1/3 = 9/27 = 25/75. The portion of the handful that was yellow is 9/18 = 1/2 = 50/100 = 3/6 = 50% = 0.5. The portion of the handful that was white is 3/18 = 1/6 = 6/36 = 10/60. Assessment Connections Questioning . . . Open with . . . How can you represent the handful of marbles as a fraction and a decimal? Probe further with . . . What information do you need to know to describe the relationship of the marbles? What fractional part have you drawn? Are there other ways to describe this fractional part? What are they? What decimal can you use to describe the relationship of the marbles? How do you find decimal equivalents? What strategies did you use to create decimal equivalents? How can you check to see if your strategy worked? How did your knowledge of equivalent fractions help you determine equivalent decimals? Listen for . . . Can the student verbalize the strategies used? Is the student using grade-appropriate language to describe fractions and decimals? Can the student describe a process for generating equivalent forms of rational numbers? Can the student explain his or her reasoning? Look for . . . Can the student write a ratio that describes the handful of marbles to the total number of marbles in the jar? Can the student write other ratios to describe other relationships between the marbles? Can the student generate equivalent forms for a rational number? Does the student have a strategy for generating equivalent forms for a rational number? Can the student use fractions to generate decimals and other fractions, and decimals to generate fractions and other decimals? Why 0 is Rational The answer to this question is that there is no answer. By this we simply mean that there is no number which, when multiplied by 0, gives you 9. The question "what is 9 divided by 0" is simply another way of asking the question "which number, when multiplied by 0, gives you 9?" There is no such number, and therefore no answer to the question. This is not simply a quirk of our usual number system: in any number system that satisfies certain basic properties such as distributivity and associativity, 0 multiplied by anything will give 0. So if you start with any non-zero number x, there cannot be any number which when multiplied by 0 gives you x, so there can be no answer to the question "what is x divided by 0". Mathematicians say that "division by 0 is undefined", meaning there is no way to define an answer to the question in any reasonable or consistent manner. It is well known that you cannot divide a number by zero. Math teachers write, for example, 24 ÷ 0 = undefined. They use analogies to convince students that it is impossible and meaningless, that “you cannot divide something by nothing.” Yet we also learn that we can multiply by zero, add zero, and subtract zero. And some teachers explain that zero is not really nothing, that it is just a number with definite and distinct properties. So, why not divide by zero? In the past, many mathematicians did. In 628 CE, the Indian mathematician and astronomer Brahmagupta claimed that “zero divided by a zero is zero.” At around 850 CE, another Indian mathematician, Mahaveera, more explicitly argued that any number divided by zero leaves that number unchanged, so then, for example, 24 ÷ 0 = 24. Later, around 1150, the mathematician Bhaskara gave yet another result for such operations. He argued that a quantity divided by zero becomes an infinite quantity. This idea persisted for centuries, for example, in 1656, the English mathematician John Wallis likewise argued that 24 ÷ 0 = ∞, introducing this curvy symbol for infinity Wallis wrote that for ever smaller values of n, the quotient 24 ÷ n becomes increasingly larger (e.g., 24 ÷ .001 = 24,000), and therefore he argued that it becomes infinity when we divide by zero. The common attitude toward such old notions is that past mathematicians were plainly wrong, confused or “struggling” with division by zero. But that attitude disregards the extent to which even formidably skilled mathematicians thoughtfully held such notions. In particular, the Swiss mathematician,Leonard Euler is widely admired as one of the greatest mathematicians in history, having made extraordinary contributions to many branches of mathematics, physics, and astronomy in hundreds of masterful papers written even during his years of blindness. Euler’s Complete Introduction to Algebra (published in German in 1770) has been praised as the most widely published book in the history of algebra. We here include the pages, in German and from an English translation, in which Euler discussed division by zero. He argued that it gives infinity. A common and reasonable view is that despite his fame, Euler was clearly wrong because if any number divided by zero gives infinity, then all numbers are equal, which is ridiculous. For example: if 3 ÷ 0 = ∞, and 4 ÷ 0 = ∞, then ∞ x 0 = 3, and ∞ x 0 = 4. Here, a single operation, ∞ x 0, has multiple solutions, such that apparently 3 = 4. This is absurd, so one might imagine that there was something “pre-modern” in Euler’s Algebra, that the history of mathematics includes prolonged periods in which mathematicians had not yet found the right answer to certain problems. However, Euler had fair reasons for his arguments. Multiple solutions to one equation did not seem impossible. Euler argued, for one, that the operation of extracting roots yields multiple results. For example, the number 1 has three cube roots, any of which, multiplied by itself three times, produces 1. Today all mathematicians agree that root extraction can yield multiple results. So why not also admit multiple results when multiplying zero by infinity? An alternate way to understand the historical disagreements over division by zero is to say that certain mathematical operations evolve over time. In antiquity, mathematicians did not divide by zero. Later, some mathematicians divided by zero, obtaining either zero or the dividend (e.g., that 24 ÷ 0 = 24). Next, other mathematicians argued, for centuries, that the correct quotient is actually infinity. And nowadays again, mathematicians teach that division by zero is impossible, that it is “undefined.” But ever since the mid-1800s, algebraists realized that certain aspects of mathematics are established by convention, by definitions that are established at will and occasionally refined, or redefined. If so, might the result of division by zero change yet again?
Representing Rational numbers On Number line Activity How to do the activity A horizontal line with an infinite sequence of equi-spaced points identified with N on its right side is called the number line. By definition, a number is just a point on the number line. In sections (A)–(K), we will use only the number line to the right of 0. We will make use of the complete number line starting in (L) when we get to negative numbers. Fractions are a special class of numbers constructed in the manner below. If a and b are two points on the number line, with a to the left of b, we denote the segment from a to b by [a, b]. The points a and b are called the endpoints of [a, b]. The special case of the segment [0, 1] occupies a distinguished position in the study of fractions; it is called the unit segment. The point 1 is called the unit. As mentioned above, 0 and 1 determine the points we call the whole numbers. So if 1 stands for an orange, 5 would be 5 oranges, and if 1 stands for 5 pounds of rice, then 6 would be 30 pounds of rice. And so on. We take as our “whole” the unit segment [0, 1]. The fraction 1 is therefore
one-third of the whole, i.e., if we divide [0, 1] into 3 equal parts, 3 stands for one of the parts. One obvious example is the thickened segment below, and we use the right endpoint of this segment as the standard representation of 1
We next divide, not just [0, 1], but every segment between two consecutive
whole numbers — [0, 1], [1, 2], [2, 3], [3, 4], etc. — into three equal parts. Then
these division points, together with the whole numbers, form an infinite sequence
of equi-spaced points, to be called the sequence of thirds. In general, a fraction
m /n S for some whole number m, which intuitively stands for “m copies of thirds”,
has the standard representation consisting of m adjoining short segments
abutting 0, where a short segment refers to a segment between consecutive points
5 in the sequence of thirds. Since we may identify this standard representation of
3 with its right endpoint, we denote the latter simply by 3 . The case of m = 10
is shown below:
Having identified each standard representation of m with its right endpoint, 3
each point in the sequence of thirds now acquires a name, as shown below. These
are exactly the fractions with denominator equal to 3.
If we consider all the fractions with denominator equal to n, then we would be led to the sequence of n-ths, which is the sequence of equi-spaced points resulting from dividing each of [0, 1], [1, 2], [2, 3], . . . , into n equal parts. The fraction m is then the m-th point to the right of 0 in this sequence. For example, the fractions with denominator equal to 5 are now displayed as shown: To find equivalent forms of Rational Numbers
Sub theme:Irrational Numbers Principal Roots and Irrational Numbers Prerequisite Concepts: Set of rational numbers
Objectives:
In this lesson, you are expected to:
1. describe and define irrational numbers;
2. describe principal roots and tell whether they are rational or irrational;
3. determine between what two integers the square root of a number is;
4. estimate the square root of a number to the nearest tenth;
5. illustrate and graph irrational numbers (square roots) on a number line with and without appropriate technology.
NOTE TO THE TEACHER
This is the first time that students will learn about irrational numbers. Irrational numbers are simply numbers that are not rational. However, they are not easy to determine, hence we limit our discussions to principal nth roots, particularly square roots. A lesson on irrational numbers is important because these numbers are often encountered. While the activities are meant to introduce these numbers in a non-threatening way, try not to deviate from the formal discussion on principal nth roots. The definitions are precise so be careful not to overextend or over generalize.
Activities
Take a look at the unusual wristwatch and answer the questions below.
1. Can you tell the time? 2. What time is shown in the wristwatch? 3. What do you get when you take the 4. How will you describe the result? 5. Can you take the exact value of √13 6. What value could you get?
PRINCIPAL ROOTS AND IRRATIONAL NUMBERS
TEACHING IDEAS NOTE TO THE TEACHER In this part of the lesson, the square root of a number is used to introduce a new set of numbers called the irrational numbers. Take not of the two ways by which irrational numbers are described and defined. Taking the square root of a number is like doing the reverse operation of squaring a number. For example, both 7 and -7 are square roots of 49 since 7 2 = 49 and ( −7) = 49 . Integers such as 1, 4, 9, 16, 25 and 36 are called perfect squares. Rational numbers such as 0.16,and 4.84 are also, perfect squares. Perfect squares are numbers that have rational numbers as square roots. The square roots 100 of perfect squares are rational numbers while the square roots of numbers that are not perfect squares are irrational numbers.
Any number that cannot be expressed as a quotient of two integers is an irrational number. The numbers 2 , π, and the special number e are all irrational numbers. Decimal numbers that are non-repeating and non-terminating are irrational numbers.
NOTE TO THE TEACHER The transition from the concept of two square roots of a positive number to that of the principal nth root has always been a difficult one for students. The important and precisely stated concepts are in bold so that students pay attention to them. Solved problems that are meant to illustrate certain procedures and techniques in determining whether a principal root is rational or irrational, finding two consecutive integers between which the irrational number is found, estimating the value of irrational square roots to the nearest tenth, and plotting an irrational square root on a number line. On Principal nth Roots Any number, say a, whose nth power (n, a positive integer), is b is called the nth root of b. Consider the following: ( −7) = 49 , 2 4 = 16 and ( −10) = −1000 . This means that -7 is a 2nd or square root of 49, 2 is a 4th root of 16 and -10 is a 3rd or cube root of -1000.
However, we are not simply interested in any nth root of a number; we are more concerned about the principal nth root of a number.
The principal n root of a positive number is the positive n root. The principal n root of a negative number is the negative nth root if n is odd. If n is even and the number is negative, the principal nth root is not defined. The notation for the principal nth root of a number b is n b . In this expression, n is the index and b is the radicand. The nth roots are also called radicals. Classifying Principal nth Roots as Rational or Irrational Numbers To determine whether a principal root is a rational or irrational number, determine if the radicand is a perfect nth power of a number. If it is, then the root is rational. Otherwise, it is irrational.
Activity to find square root using geoboard
How Irrational! In this lesson, students use geoboards to construct non-traditional, "tilted" squares whose side lengths are irrational numbers. This lesson addresses standards in both Number Sense and Measurement.
Learning Objectives Students will: Estimate square roots to the nearest whole number without a calculator Relate squaring a number and finding square root as inverse operations Define irrational number and give examples Materials
10 × 10 geoboards with elastics
Internet access to a virtual geoboard or overhead geoboardDot Paper Chart or Poster Paper Instructional Plan Begin by having students evaluate expressions involving square roots. Review the notation for square root and the geometric meaning of square root, which is the length of a side of a square with a given area. Construct these triangles on a virtual geoboard. Provide students with the formula for the area of a triangle (A = ½bh) and ask them to determine the areas of the displayed triangles. [12.5 units2 and 4.5 units2.]
Tell students that there are more squares that fit on a geoboard than those found during the previous lesson. Today's lesson will focus on finding some atypical squares using geoboards. Discuss the questions on the overhead. Ask, "How can we determine the area of the square?" [One possible method is to construct a square that surrounds this square; determine the area of the four corner triangles, and subtract the area of the large, outer square minus the area of the four triangles.] Students may need a review on finding the area of a triangle. Also, introduce the term irrational number. An irrational number can be understood as the side length of a square whose area is not a perfect square. For example, 5 is not a perfect square. Therefore, the square root of 5 is an irrational number. In other words, there is no rational number that, when squared, is equal to 5. Have students work in groups of four to find more squares with non-horizontal, non-vertical sides using geoboards. Although the students have their own geoboards, group interaction will promote communication and provide peer support for this challenging mathematical conc
Questions for Students Is there more than one way to determine the area of the square? [Break the square into parts.] Once you know the area of a square, how can you find the side length? [Take the square root of the area.] Explain how you estimated square roots to the nearest whole number. [Answers will vary. Encourage answers such as: the square root of 15 rounds to 4, since 15 is between 9 (32) and 16 (42), but closer to 16. Therefore, the square root of 15 rounds to 4.] For the activity see http://illuminations.nctm.org/LessonDetail.aspx?ID=L833 Activity Representing an irrational number on a number line Part(2)
Learn how to represent √2 on a number line. 1. First of all draw the number line. 2. Mark point A at "0" and B at "1". This means AB = 1 Unit. 3. Now, at B, draw BX perpendicular to AB. 4. Cut off BC = 1 Unit. 5. Join AC. 6. By Pythagoras theorem in right triangle ABC, we get AC = √2 Units. 7. Now, with radius AC and centre A, mark a point on the number line. Let the marked point is M. M represents √2 on the number line.
TOPIC:NUMBER SYSTEM![]()
![]()

![]()
![]()
![]()

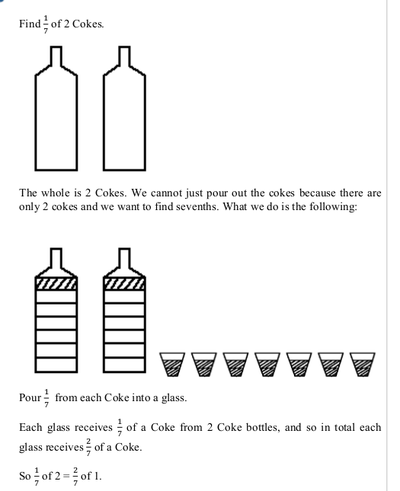

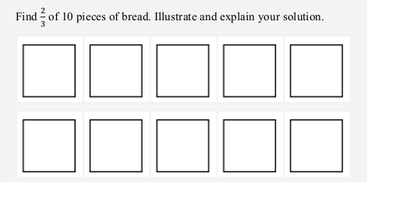 File:Number system -Resource material_html_58f2d11d.png
File:Number system -Resource material_html_58f2d11d.png

Teachers Corner
GeoGebra Contributions
- The GeoGebra file below demonstrates Integer Addition
- Integer Addition http://karnatakaeducation.org.in/KOER/Maths/Integer_Addition.html
- Download ggb file here http://karnatakaeducation.org.in/KOER/Maths/Integer_Addition.ggb
- The GeoGebra file below demonstrates Sum of Natural Numbers
- corresponding angles http://karnatakaeducation.org.in/KOER/Maths/natsum.html
- Download ggb file here http://karnatakaeducation.org.in/KOER/Maths/natsum.ggb
- See a video for a proof by induction http://www.youtube.com/watch?v=WHVOLY9mrJ4