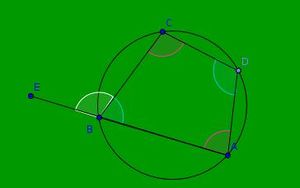
Properties of cyclic quadrilateral
Revision as of 11:55, 5 November 2019 by Vedavathi (talk | contribs) (added Category:Circles using HotCat)
Relation between the angles of a cyclic quadrilateral are explored with this hand on activity.
Objectives
- In a cyclic quadrilateral the sum of opposite interior angles is 180 degrees.
- In a cyclic quadrilateral the exterior angle is equal to interior opposite angle
Estimated Time
45 minutes
Prerequisites/Instructions, prior preparations, if any
- Circles and quadrilaterals should have been covered.
Materials/ Resources needed
Non digital: Coloured paper, pair if scissors, sketch pen, carbon paper, geometry box
This activity has been taken from the website http://mykhmsmathclass.blogspot.in/2007/11/class-ix-activity-16.html
Process (How to do the activity)
Note: Refer the above geogebra file to understand the below mentioned labelling.,br>
- Draw a circle of any radius on a coloured paper and cut it.
- Paste the circle cut out on a rectangular sheet of paper.
- By paper folding get chords AB, BC, CD and DA in order.
- Draw AB, BC, CD & DA. A cyclic quadrilateral ABCD is obtained.
- Make a replica of cyclic quadrilateral ABCD using carbon paper.
- Cut the replica into 4 parts such that each part contains one angle .
- Draw a straight line on a paper.
- Place angle BAD and angle BCD adjacent to each other on the straight line.Write the observation.
- Place angle ABC and angle ADC adjacent to each other on the straight line . Write the observation.
- Produce AB to form a ray AE such that exterior angle CBE is formed.
- Make a replica of angle ADC and place it on angle CBE . Write the observation.
- Developmental Questions (What discussion questions)
- How do you take radius ?
- What is the circumference ?
- What is a chord ?
- What is a quadrilateral ?
- Where are all four vertices of a quadrilateral located ?
- What part are we trying to cut and compare ?
- What can you infer ?
- Evaluation Questions
- Angle BAD and angle BCD, when placed adjacent to each other on a straight line, completely cover the straight angle.What does this mean ?
- Angle ABC and angle ADC, when placed adjacent to each other on a straight line, completely cover the straight angle.What can you conclude ?
- Compare angle ADC with angle CBE.
- Name the two properties of cyclic quarilaterals.