Difference between revisions of "Universal Law of Gravitation"
(Created page with "{{subst:Science-Content}}") |
|||
| Line 31: | Line 31: | ||
= Teaching Outlines = | = Teaching Outlines = | ||
| − | ==Concept #== | + | '''Newton's law of universal gravitation''' |
| + | |||
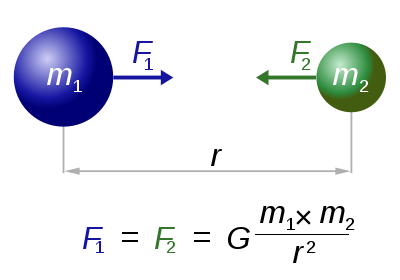
| + | Newton's law of universal gravitation states that every particle in the universe attracts every other particle with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between them. This force acts along the line joining the two particles. | ||
| + | |||
| + | Separately it was shown that large spherically symmetrical masses attract and are attracted as if all their mass were concentrated at their centres. | ||
| + | |||
| + | For non-symmetric objects, the masses will be concentrated a the centre of mass and the distance between these centres is what will be taken as the distance | ||
| + | |||
| + | |||
| + | [[Image:Gravitation%20for%20wiki_html_39d0b1a1.png]] <br> | ||
| + | |||
| + | F = G m1m2 / r2 | ||
| + | |||
| + | * F is the force between the masses, | ||
| + | * m1 is the first mass, | ||
| + | * m2 is the second mass, | ||
| + | * G is the gravitational constant | ||
| + | * r is the distance between the masses | ||
| + | |||
| + | In SI units, Force, F is measured in newtons (N), masses m1 and m2 are measured in kilograms (kg), and the distance between the masses is measured in metres. | ||
| + | <br><br> | ||
| + | |||
| + | === Activity 1 Use the following simulation for a demonstration of the gravitational force === | ||
| + | |||
| + | [http://phet.colorado.edu/en/simulation/gravity-force-lab Click here for PhET simulation] | ||
| + | <br><br> | ||
| + | |||
| + | '''Universal Gravitational Constant''' | ||
| + | |||
| + | The magnitude of G is identical to the magnitude of the force between a pair of 1-kg masses that are 1 metre apart and has been experimentally determined to be equal to 6.674×10−11N m2 kg−2. The value of the constant G was first accurately determined from the results of an experiment conducted by the British scientist Henry Cavendish in 1798. He accomplished by measuring the tiny force between lead masses with an extremely sensitive torsion balance. | ||
| + | |||
| + | This small magnitude indicates that the gravitational force is an extremely weak force. | ||
| + | |||
| + | This experiment was also the first test of Newton's theory of gravitation between masses in the laboratory. It took place 111 years after the publication of Newton's Principia and 71 years after Newton's death, so none of Newton's calculations could use the value of G; instead he could only calculate a force relative to another force. | ||
| + | <br><br>'''Inverse Square Law''' | ||
| + | |||
| + | Newton's law of gravitation resembles Coulomb's law of electrical forces, which is used to calculate the magnitude of electrical force between two charged bodies. Both are inverse-square laws, in which force is inversely proportional to the square of the distance between the bodies. Coulomb's Law has the product of two charges in place of the product of the masses, and the electrostatic constant in place of the gravitational constant. One important point of comparison is that the the value of the constant in Coulomb's law (for force between two charges of 1C separated by a distance of 1 m) is of the order of magnitude 109, which is 1000 billion billion times more than the gravitational constant. This means that the electrostatic force is a much stronger force than the gravitational force. | ||
| + | |||
| + | '''Why should this be so?''' | ||
| + | |||
| + | |||
| + | |||
| + | [[Image:Gravitation%20for%20wiki_html_m1eae328e.png]] <br> | ||
| + | |||
| + | |||
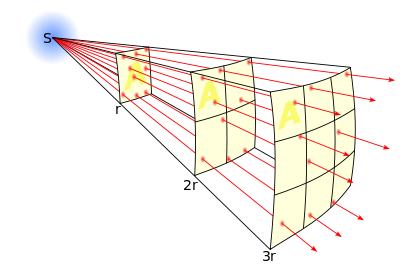
| + | When we consider the gravitational field of a mass, we consider it to be a point mass. For any object, this can be approximated and we can find that this holds true. Some standard physics textbooks will give us this mathematical derivation as well. If there is a point mass and there is a field originating from it, the field must originate uniformly in all directions. If we imagine enclosing this point mass in a sphere and if we represent the field by field lines (called flux), we can visualize that these field lines must pass through uniformly throughout the surface area of the sphere. Now we can use simple geometry to explain why the field varies with inverse square of the distance. For the same area, the number of flux lines that will cut through a given area will reduce the farther the area is from the source. If we consider the area as a square on the surface of a sphere, the density of flux lines that will cut through the surface of a sphere is inversely proportional to the square of the distance from the source as the surface area of a sphere increases with the square of the radius. Hence the field strength will vary inversely with the square of the distance. | ||
| + | <br><br>'''Law of gravitation and relativity''' | ||
| + | |||
| + | Newton's law has since been superseded by Einstein's theory of general relativity, but it continues to be used as it is, as an excellent approximation of the effects of gravity. Gravitational force acts at a distance. The properties of the space surrounding any massive body can be considered to be altered in such a way that another massive body in this region experiences a force. This alteration of space is a gravitational field. Einstein perceived a gravitational field as a geometrical warping of four dimensional space and time; masses “bend” the space around them. Gravity is the property of matter that possesses mass that causes a force of attraction to exist between any two particles in space. | ||
| + | <br> | ||
| + | |||
| + | ==Concept #1 - Nature of Gravitational Force == | ||
===Learning objectives=== | ===Learning objectives=== | ||
| + | #Inertial and Gravitational Property of Mass | ||
| + | #Idea of a force field and that forces can act at a distance. The distance over which the effect of a force can be felt is called its field. | ||
| + | #Gravitational force acts over a distance through a field and is one of the four fundamental forces | ||
| + | #Gravitational force is a very small force | ||
| + | |||
===Notes for teachers=== | ===Notes for teachers=== | ||
''These are short notes that the teacher wants to share about the concept, any locally relevant information, specific instructions on what kind of methodology used and common misconceptions/mistakes.'' | ''These are short notes that the teacher wants to share about the concept, any locally relevant information, specific instructions on what kind of methodology used and common misconceptions/mistakes.'' | ||
| + | * Mass has two aspects – inertial and gravitational. We are familiar with mass; it is an intrinsic property of matter. An intrinsic property is something that cannot be separated from the object. The mass of an object can be understood in terms of its gravitational aspect and inertial aspect. The intrinsic property of matter which makes it resist change is what we have called as mass. But this same mass possesses another property – the ability to “attract” mass. This we call the gravitational aspect. The gravitational aspect of the mass is responsible for the attractive force between two masses. The gravitational aspect is what makes masses interact with one another.<br> | ||
| + | |||
| + | * Gravitation is a fundamental force. Gravitational force, or gravity, is the force by which physical bodies attract each other with a force directly proportional to their mass and inversely proportional to the square of the distance between them. This is one of the four fundamental forces in nature. Gravity is the force which makes masses interact with one another. Gravitational force is mutually attractive. Another fundamental force is the electromagnetic force, due to another intrinsic property of matter – charge. These forces are due to charges possessed by an object and their movement.<br> | ||
| + | * Strong and weak nuclear forces are other fundamental forces that act within the nucleus of an atom, holding it together. These forces however act only at the subatomic level. Above the atomic level, gravitational and electromagnetic forces can satisfactorily explain all events. | ||
| + | <br><br> | ||
| + | |||
===Activity No # === | ===Activity No # === | ||
{| style="height:10px; float:right; align:center;" | {| style="height:10px; float:right; align:center;" | ||
Revision as of 19:47, 3 December 2013
| Philosophy of Science |
While creating a resource page, please click here for a resource creation checklist
Concept Map
Textbook
To add textbook links, please follow these instructions to: (Click to create the subpage)
Additional information
Useful websites
Reference Books
Teaching Outlines
Newton's law of universal gravitation
Newton's law of universal gravitation states that every particle in the universe attracts every other particle with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between them. This force acts along the line joining the two particles.
Separately it was shown that large spherically symmetrical masses attract and are attracted as if all their mass were concentrated at their centres.
For non-symmetric objects, the masses will be concentrated a the centre of mass and the distance between these centres is what will be taken as the distance
F = G m1m2 / r2
- F is the force between the masses,
- m1 is the first mass,
- m2 is the second mass,
- G is the gravitational constant
- r is the distance between the masses
In SI units, Force, F is measured in newtons (N), masses m1 and m2 are measured in kilograms (kg), and the distance between the masses is measured in metres.
Activity 1 Use the following simulation for a demonstration of the gravitational force
Click here for PhET simulation
Universal Gravitational Constant
The magnitude of G is identical to the magnitude of the force between a pair of 1-kg masses that are 1 metre apart and has been experimentally determined to be equal to 6.674×10−11N m2 kg−2. The value of the constant G was first accurately determined from the results of an experiment conducted by the British scientist Henry Cavendish in 1798. He accomplished by measuring the tiny force between lead masses with an extremely sensitive torsion balance.
This small magnitude indicates that the gravitational force is an extremely weak force.
This experiment was also the first test of Newton's theory of gravitation between masses in the laboratory. It took place 111 years after the publication of Newton's Principia and 71 years after Newton's death, so none of Newton's calculations could use the value of G; instead he could only calculate a force relative to another force.
Inverse Square Law
Newton's law of gravitation resembles Coulomb's law of electrical forces, which is used to calculate the magnitude of electrical force between two charged bodies. Both are inverse-square laws, in which force is inversely proportional to the square of the distance between the bodies. Coulomb's Law has the product of two charges in place of the product of the masses, and the electrostatic constant in place of the gravitational constant. One important point of comparison is that the the value of the constant in Coulomb's law (for force between two charges of 1C separated by a distance of 1 m) is of the order of magnitude 109, which is 1000 billion billion times more than the gravitational constant. This means that the electrostatic force is a much stronger force than the gravitational force.
Why should this be so?
When we consider the gravitational field of a mass, we consider it to be a point mass. For any object, this can be approximated and we can find that this holds true. Some standard physics textbooks will give us this mathematical derivation as well. If there is a point mass and there is a field originating from it, the field must originate uniformly in all directions. If we imagine enclosing this point mass in a sphere and if we represent the field by field lines (called flux), we can visualize that these field lines must pass through uniformly throughout the surface area of the sphere. Now we can use simple geometry to explain why the field varies with inverse square of the distance. For the same area, the number of flux lines that will cut through a given area will reduce the farther the area is from the source. If we consider the area as a square on the surface of a sphere, the density of flux lines that will cut through the surface of a sphere is inversely proportional to the square of the distance from the source as the surface area of a sphere increases with the square of the radius. Hence the field strength will vary inversely with the square of the distance.
Law of gravitation and relativity
Newton's law has since been superseded by Einstein's theory of general relativity, but it continues to be used as it is, as an excellent approximation of the effects of gravity. Gravitational force acts at a distance. The properties of the space surrounding any massive body can be considered to be altered in such a way that another massive body in this region experiences a force. This alteration of space is a gravitational field. Einstein perceived a gravitational field as a geometrical warping of four dimensional space and time; masses “bend” the space around them. Gravity is the property of matter that possesses mass that causes a force of attraction to exist between any two particles in space.
Concept #1 - Nature of Gravitational Force
Learning objectives
- Inertial and Gravitational Property of Mass
- Idea of a force field and that forces can act at a distance. The distance over which the effect of a force can be felt is called its field.
- Gravitational force acts over a distance through a field and is one of the four fundamental forces
- Gravitational force is a very small force
Notes for teachers
These are short notes that the teacher wants to share about the concept, any locally relevant information, specific instructions on what kind of methodology used and common misconceptions/mistakes.
- Mass has two aspects – inertial and gravitational. We are familiar with mass; it is an intrinsic property of matter. An intrinsic property is something that cannot be separated from the object. The mass of an object can be understood in terms of its gravitational aspect and inertial aspect. The intrinsic property of matter which makes it resist change is what we have called as mass. But this same mass possesses another property – the ability to “attract” mass. This we call the gravitational aspect. The gravitational aspect of the mass is responsible for the attractive force between two masses. The gravitational aspect is what makes masses interact with one another.
- Gravitation is a fundamental force. Gravitational force, or gravity, is the force by which physical bodies attract each other with a force directly proportional to their mass and inversely proportional to the square of the distance between them. This is one of the four fundamental forces in nature. Gravity is the force which makes masses interact with one another. Gravitational force is mutually attractive. Another fundamental force is the electromagnetic force, due to another intrinsic property of matter – charge. These forces are due to charges possessed by an object and their movement.
- Strong and weak nuclear forces are other fundamental forces that act within the nucleus of an atom, holding it together. These forces however act only at the subatomic level. Above the atomic level, gravitational and electromagnetic forces can satisfactorily explain all events.
Activity No #
- Estimated Time
- Materials/ Resources needed
- Prerequisites/Instructions, if any
- Multimedia resources
- Website interactives/ links/ simulations
- Process (How to do the activity)
- Developmental Questions (What discussion questions)
- Evaluation (Questions for assessment of the child)
- Question Corner
Activity No #
- Estimated Time
- Materials/ Resources needed
- Prerequisites/Instructions, if any
- Multimedia resources
- Website interactives/ links/ simulations
- Process (How to do the activity)
- Developmental Questions (What discussion questions)
- Evaluation (Questions for assessment of the child)
- Question Corner
Concept #
Learning objectives
Notes for teachers
These are short notes that the teacher wants to share about the concept, any locally relevant information, specific instructions on what kind of methodology used and common misconceptions/mistakes.
Activity No #
- Estimated Time
- Materials/ Resources needed
- Prerequisites/Instructions, if any
- Multimedia resources
- Website interactives/ links/ simulations
- Process (How to do the activity)
- Developmental Questions (What discussion questions)
- Evaluation (Questions for assessment of the child)
- Question Corner
Activity No #
- Estimated Time
- Materials/ Resources needed
- Prerequisites/Instructions, if any
- Multimedia resources
- Website interactives/ links/ simulations
- Process (How to do the activity)
- Developmental Questions (What discussion questions)
- Evaluation (Questions for assessment of the child)
- Question Corner
Project Ideas
Fun corner
Usage
Create a new page and type {{subst:Science-Content}} to use this template