Number System
- Back to Mathematics Portal
- Back to Topics in School Mathematics
- Resource Creation Checklist - for guidelines on how to add resources.
Concept Map
Textbook
To add textbook links, please follow these instructions to: (Click to create the subpage)
Additional Information
Useful websites
Watch the following video on the story of how numbers evolved. The video called Story of One tells how numbers evolved and the initial questions around number theory.
This video is related to number system, helps to know the basic information about number system
Reference Books
Teaching Outlines
Concept #1 - History of Numbers: Level 0
Learning objectives
- What is the story of numbers?
- How did counting begin and learning distinguish between the quantity 2 and the number 2.
- The number "2" is an abstraction of the quantity
Notes for teachers
These are short notes that the teacher wants to share about the concept, any locally relevant information, specific instructions on what kind of methodology used and common misconceptions/mistakes.
Activities
- Activity Template
- Activity 1
Concept #2 Number Sense and Counting : Level 0
Objectives
1. Understand that there is an aspect of quantity that we can develop with disparate objects
2. Comparison and mapping of quantities (more or less or equal)
3. Representation of quantity by numbers and learning the abstraction that “2 represents quantity 2 of a given thing”
4. Numbers also have an ordinal value – that of ordering and that is different from the representation aspect of numbers
5. Expression of quantities and manipulation of quantities (operations) symbolically
6. Recognizing the quantity represented by numerals and discovering how one number is related to another number
7. This number representation is continuous.
Notes for teachers
This is not one period – but a lesson topic. There could be a few more lessons in this section. For example, for representing collections and making a distinction between 1 apple and a dozen apples. This idea could be explained later to develop fractions. Another activity that can also be used to talk of units of measure. Addition and subtraction have been discussed here – extend this to include multiplication and division).
Activities
- Activity 1 - Quantity and Numbers
- The Eighth Donkey Story
- Activity 2 - Cardinal and Ordinal Numbers
Concept #3 The Number Line :Level 1-2
Objectives
- Numbers can be represented on a continuum called a number line
- Number line is a representation; geometric model of all numbers
- Mathematical operations can b explained by moving along the number line
Notes for teachers
Introduce the number line as a concept by itself as well as a method to count, measure and perform arithmetic operations by moving along the number line through different activities.
Activities
- Activity 1 - To introduce Number line
- Activity 2 - Sum and product of numbers 1
- Activity 3 - Classroom number line
Concept #4 Number Bases
Learning objectives
Notes for teachers
These are short notes that the teacher wants to share about the concept, any locally relevant information, specific instructions on what kind of methodology used and common misconceptions/mistakes.
Activities
- Activity 1 - Activity-1
- Activity 2 - Activity-2
Concept #4 Place Value
I Making hundreds, tens and ones (1 period)

- Print 32 squares of this.
- Distribute into 8 groups of 4 children each.
- Each group will get 4 squares.
- The value of 4 squares will be 4x100 = 400
- Each group must cut the solid lines; 1 square will have 10 strips. These are tens. So each square has 10 “tens” (They can either *cut, or work without cutting – up to the children)
- Each one of those tens will have 10 ones.
- Let the children make numbers and write them down
- Ask them what is the largest number each group can make? 400 is the answer – but check if children understand this.
II. Abstraction from here (1 period)
Now let us assume children have 9 such squares.
In each group, how many hundreds are possible ? – 9
In each group, how many tens are there ? – 9 x 10 = 90
In each group, how many tens are there ? – 90 x 10 = 900
1-9 ones are possible; 10 ones means one ten. Ten ones is the same as one ten
1-9 tens are possible; 10 tens means one hundred. Ten tens is the same as one hundred.
What happens when we have 10 hundreds? What is it the same as?
What is the importance of ten? We count in groups of tens
9+1= 10 = 10 x 1
99 + 1 = 100 = 10 x 10
999 + 1 = 1000 = 10 x 100
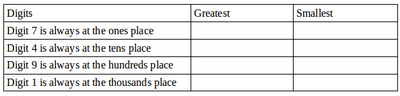
Greatest 1-digit number + 1 = Smallest 2-digit number
Greatest 2-digit number + 1 = Smallest 3-digit number
Greatest 3-digit number + 1 = Smallest 4-digit number
Following the pattern, we can expect that, on adding 1 to the greatest 4-digit number
(9999 – nine thousand nine hundred and ninety nine) we get the smallest 5-digit number
(9999 + 1 = 10,000 or ten thousand). Further we can expect that 10 x 1000 = 10,000 i.e.
9999 + 1 = 10,000 = 10 x 1000.
Do this only when children are confident – this is for advanced students
Write on the board like this:
| Hundreds | Tens | Ones | Number | Comments |
|---|---|---|---|---|
| 3 | 8 | 3 | 383 | Watch if students are stating numbers are correct |
| 4 | 7 | 2 | Watch if students are stating numbers are correct | |
| 0 | 3 | 5 | Ask how many hundreds there are? They should say this number is less than hundred | |
| 1 | 10 | 5 | Do they say 205? What is the answer? | |
| 2 | 8 | 3 | Without forming the number can they say if number >200? Can they say if this is greater than number below? | |
| 2 | 7 | 5 | Without forming the number can they say if number >200? | |
| 10 | 7 | 3 | What is the answer here?Point out “regrouping”. This is important for addition/ subtraction | |
| 11 | 8 | 2 | What is the answer here? Think about how students are doing 10 hundreds plus 1 hundred. Point out “regrouping”. This is important for addition/ subtraction | |
| 1 | 7 | 4 | 3 | Without forming the number can they say if number >200? |
III. Fill number line (1 period)
Draw these one below the other
1,2,.......
10,20,.......
100, 200,.....
IV Tell stories and Play With Number Systems (1 period - optional)
http://www.math.wichita.edu/history/topics/num-sys.html#sense
(This page is downloaded and given as reading materials – page is called Number Systems)
V Questions/ activities for class
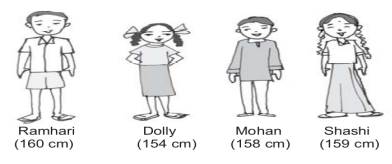
- Arrange in order – shortest, tallest, increasing and decreasing order
- Making numbers
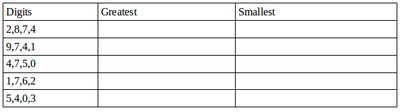
Suppose we have 4 digits 7, 8, 3, 5. We want to make different 4-digit numbers using these digits such that no digits are repeated in each number. For example, you can make 7835 and 3578 but 7738 is not allowed because 7 is repeated and 5 is not used.
a. What is the greatest number you can make?
b. What is the smallest number?
c. Can you write down how you make the greatest number and the smallest number?
Use the given digits without repetition and make the greatest and smallest 4-digit numbers. Note that 0753 is a 3 digit number and is therefore not allowed.
- Now make the greatest and smallest 4-digit numbers by using any one digit twice.
Hint: Think about which digit you will use twice.
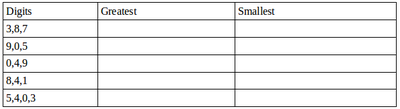
- Make the greatest/ smallest 4-digit numbers using any 4 different digits with conditions as given
Learning objectives
Notes for teachers
These are short notes that the teacher wants to share about the concept, any locally relevant information, specific instructions on what kind of methodology used and common misconceptions/mistakes.
Activities
- Activity 1 Activity-1
- Activity 2 Activity-2
Concept #3 Negative numbers are the opposite of positive numbers -
Objectives
- To extend the understanding and skill of representing symbolically numbers and manipulating them.
- To understand that negative numbers are numbers that are created to explain situations in such a way that mathematical operations hold
- Negative numbers are opposite of positive numbers; the rules of working with negative numbers are opposite to that of working with positive numbers
- Together, the negative numbers and positive numbers form one contiuous number line
- Perform manipulations with negative numbers and express symbolically situations involving negative numbers
Notes for teachers
Negative numbers are to be introduced as a type of number; they do the opposite of what positive numbers do.
Read the activity for more detailed description.
Activities
- Activity 1 -What are negative numbers
Sub Theme:Fractions Introduction: Fractions are defined in relation to a whole—or unit amount—by dividing the whole into equal parts. The notion of dividing into equal parts may seem simple, but it can be problematic. Although we use pairs of numbers to represent fractions, a fraction stands for a single number, and as such, has a location on the number line. Number lines provide an excellent way to represent improper fractions, which represent an amount that is more than the related whole. Instruction in fractions that focuses only on the mechanics of procedures and not on reasoning misses valuable opportunities to guide students in developing this core mathematical skill. This section explains the meaning of fractions, reviews some of the common difficulties in understanding the meaning of fractions, and describes how to use simple pictures to represent fractions.Fractions arise naturally whenever we want to consider one or more parts of an object or quantity that is divided into pieces. Consider how fractions are used in the following ordinary situations:
In this section, we define what we mean by a fraction is part of of an object, collection or quantity.
The five meanings listed below serve as conceptual models or tools for thinking about and working with fractions and serve as a framework for designing teaching activities that engage students in sense making as they construct knowledge about fractions.
1.Part of a whole 2.Part of a group/set 3.Measure (name for point on number line) 4.Ratio 5.Indicated divisionInterpreting fractions
Given their different representations, and the way they sometimes refer to a number and sometimes an operation, it is important to be able to discuss fractions in the many ways they appear. A multiple representation activity, including different numerical and visual representations, is one way of doing this. Sharing food is a good way to introduce various concepts aboput fractions. For example, using a chocolate bar and dividing it into pieces. This can be highly motivating if learners can eat it afterwards. A clock face shows clearly what halves and quarters look like, and can be extended to other fractions with discussion about why some are easier to show than others. We can find a third of an hour, but what about a fifth?
A paper tape measure is a valuable illustration of
different fractions. For example, learners can write on 1/2m, 0.50m and
50cm for their own portable equivalence chart.
Folding of paper also can illustrate fractions
I have ten bars of chocolate, and I share them equally between four people. How much will they each get?
We recommend that teachers explicitly use thelanguage of fractions in other
parts of the curriculum for reinforcement. For example, when looking at
shapes, talk about ‘half a square’ and ‘third of a circle’.
Assessment activities
Hints for difficult problems
Project Ideas
Math Fun
Usage
Create a new page and type {{subst:Math-Content}} to use this template