Mensuration
| Philosophy of Mathematics |
While creating a resource page, please click here for a resource creation checklist.
Concept Map
Error: Mind Map file Mensuration.mm not found
Textbook
Additional Information
Useful websites
- Download PDF. This is a good website for interesting activities on mensuration.
- For standard measurements : http://www.primaryresources.co.uk/maths/mathsE1.htm
- http://www.campusgate.co.in/2011/11/areas-and-mensuration.html
- For general rules while writing units ://en.wikipedia.org/wiki/International_System_of_Units#General_rules
- For teacher reference on dimension. http://www.britannica.com/EBchecked/topic/163641/dimension
- The metric system is enormously powerful as a standard measurement system. In this video, you can explore from the very small to the very large and appreciate what a degree of ten means!
Reference Books
Teaching Outlines
Concept #1. What is Mensuration ?
Learning objectives
- units and measurement
- Mensuration is the branch of Mathematics dealing with measurement of angles, length, area, and volume.
- There are standard and non-standard ways of measurements.
- Importance of having standardised measurements.
- The length of the total boundary of a figure is called its perimeter. The Metric unit of perimeter is same as the unit of length - Metre.
- The amount of surface covered by an object is called it area. The Metric unit of area is square metre.
- The capacity of an object to hold is called its volume.
- They should develop the ability to calculate the area, perimeter, volume or side of many different figures.
Notes for teachers
Source: http://depts.washington.edu/chemcrs/bulkdisk/chem120A_sum06/handout_CH%201-4%20TIMBER.pdf
Summary : Measurement are an important part of our everyday life. Think about your day; you probably made some measurements. Perhaps you checked your weight by stepping on a scale,measuring shoes to fit your feet in the shoe store, or saw measuring up houses when they are doing renovations etc. If you did not feel well, you may have taken your temperature. To make some soup, you added 2 cups of water to a package mix. If you stopped at the Petrol bunk, you watched the petrol pump measure the number of litres of petrol you put in the car.
Activities
Concept #2.Informal units of measurements
Learning objectives
- The traditional ways of measurements are a type of measure which uses non-standard units such as hand spans, armlengths, footsteps or pattern blocks to measure length, area, etc.
- Non-standard measurements are not always the same but vary from person to person.
Notes for teachers
- The teacher can ask the students to gather information regarding earlier traditional measuring ways from their elders and have an initial discussion in the classroom.
Activities
Concept #3. Standard units of measurements
Learning objectives
- The ability to obtain accurate measurements and communicate those measurements is a key requirement for progress.
- Standardised measuring units ensure uniformity in meaurements.
- The standard unit for length is metre, for weight id kilogram, for time is second, for temperature is Kelvin and for amount of substance it is mole.
Notes for teachers
A unit of measurement is a definite magnitude of a physical quantity, defined and adopted by convention or by law, that is used as a standard for measurement of the same physical quantity. Any other value of the physical quantity can be expressed as a simple multiple of the unit of measurement.
For example, length is a physical quantity. The metre is a unit of length that represents a definite predetermined length. When we say 10 metres (or 10 m), we actually mean 10 times the definite predetermined length called "metre".<br.
The definition, agreement, and practical use of units of measurement have played a crucial role in human endeavour from early ages up to this day. Different systems of units used to be very common. Now there is a global standard, the International System of Units (SI), the modern form of the metric system.
Activities
- Activity 1 Hunting Treasure and Measuring - Part 1
- Activity 2 Hunting Treasure and Measuring - Part 2
Concept # 4. Scale drawing
Learning objectives
- The process of representing actual distances on paper using proportional distances.
- To understand the definition and meaning of scale
- To learn about the tools of measuring
Notes for teachers
- A Scale drawing is a drawing that shows a real object with accurate sizes except they have all been reduced or enlarged by a certain amount (called the scale).
- Since it is not always possible to draw on paper the actual size of real-life objects such as the real size of a car, an airplane, we need scale drawings to represent the size.
- Drawing to scale is a tool that Engineers use for many different tasks. One key part of every scale drawing is the scaling factor. This number represents the degree to which our scale drawing or scale model has been reduced in size when compared to the original.
Activities
Concept #
Learning objectives
Notes for teachers
These are short notes that the teacher wants to share about the concept, any locally relevant information, specific instructions on what kind of methodology used and common misconceptions/mistakes.
Activities
- Activity No #1 Concept Name - Activity No.
- Activity No #2 Concept Name - Activity No.
Concept #
Learning objectives
Notes for teachers
These are short notes that the teacher wants to share about the concept, any locally relevant information, specific instructions on what kind of methodology used and common misconceptions/mistakes.
Activities
- Activity No #1 Concept Name - Activity No.
- Activity No #2 Concept Name - Activity No.
Assessment activities for CCE
Hints for difficult problems
Exercise 16.1
Problem 7.
1)Craft teacher of a school taught the students to prepare cylindrical pen holders out of card board. In a class of strength 42, if each child prepared a pen holder of radius 5 cm and height 14 cm, how much cardboard was consumed? solution
- Interpretation;
Case 1)Pen stand which is open on top and closed base. Then we have to calculate Curved surface area of cylinder and area of one circle.
- skills
visualising the cylinder into rectangle and circle
- Assumptions:
Concepts used
- basics of circles -radius
- area of circles
- addition and multiplication of fractions
- unit of area
knowledge to be used
- knowledge of Polygons -Rectangles
- knowledge of measurements
- Formula of CSA of cylinder
- substitution
- computing
- Value of Л
Concepts to be taught
- basics of circles -radius
- area of circles
- relation between circumference of circle and length of rectangle in a cylinder
- addition and multiplication of fractions
- unit of area
solution: r=5cm, h=14cm, Л=
Curved surface area of cylinder and area of one circle= CSA of cylinder+area of circle
=Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 2Лrh+Лr^2}
=
=440+78.5
=518.5cm
Cardboard required to prepare 42 penstands= 42X518.5
=
=
Case 2:- Hollow pen stand: Pen stand which is open both the sides i.e., top and base.
Then we have to calculate Curved surface area of cylinder.
Case 3:-Pen stand which is closed both the sides i.e., top and base.
Then we have to calculate total surface area of cylinder.
Activity Making use of 2200 cmcardboard sheet how many hollow cylinders of radius 7 cm and height 5 cm can be prepared.
solved problems on cone Example 10
- Find the weight of a solid cone whose base is of diameter 14 cm and vertical height 51,
cm, if the material of which it is made weighs 10gm/ Solution
- Statement of the problem:What is the weight of a solid cone whose base is of diameter 14 cm and vertical height 51cm, if the material of which it is made weighs 10gm/
- Interpretation;
Calculating the weight of solid cone by calculating its volume. density of a material is given. it is related to volume and weight.
- Assumptions:
Concepts used
- basics of circles -radius
- area of circles
- multiplication of fractions
- unit of volume,density and weight
- density
knowledge to be used
- radius=diameter/2
- density=mass/volume
- knowledge of measurements
- Formula of volume of cones
- substitution
- computing
- Value of Л
Concepts to be taught
- density
- units conversion
solution:
d=14cm r=7cm, h=51cm
Volume of cone=
=Failed to parse (syntax error): {\displaystyle \frac{1}{3}{Л}{r^2}h}
=
=
To calculate weight of the solid cone we have to use density of the given material.
density=
=
Weight of solid cone=volumeXdensity
=
=26.18Kg
problem on combination of solids example 01
Problem-03
- A Cylindrical container of radius 6cm and height 15cm is filled with ice cream. The whole ice cream has to be distributed to 10 children in equal cones with hemispherical tops. If the height
of the conical portion is 4 times the radius of its base , find the radius of the cream cones.
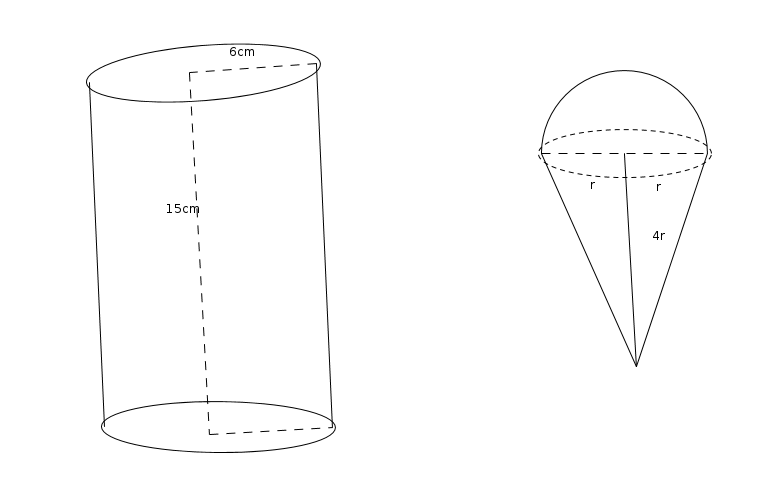
Solution
Solution
- Statement of the problem
- A Cylindrical container of radius 6cm and height 15cm is filled with ice cream. The whole ice cream has to be filled in 10 equal cones with hemispherical tops. and the height
of the conical portion is 4 times the radius of its base.
.
Assumptions
- Student should know volume of cone,and volume of Hemisphere
- Student should know the value of л=22/7
- Student should know the difference between radius and height
- Student should know the proper substitution simplification
Concepts to be taught
- Let us consider the volume of a cone having hemispherical top =2л
- Volume of Cylindrical container is equated to volume of cone having hemispherical top
Gaps
- Comparision between the volumes of cylinder and (cone+Hemisphere)
Skills
- To imagine a cone , Hemisphere,and cylinder
- To imagine a cone having Hemispherical top
Algorthem
Part 1:
To derive the volume of a cone with hemispherical top
- volume of a cone with hemispherical top
=Failed to parse (syntax error): {\displaystyle {\frac{1}{3}}л{r^2}h+{\frac{2}{3}}л{r^3}}
=Failed to parse (syntax error): {\displaystyle {\frac{1}{3}}л4r +{\frac{2}{3}}л{r^3}}
(on simplification)
=Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 2л{r^3}}
Part 2 :
To calculate the volume of 10 cone with hemispherical top
=Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 10X2л{r^3}}
=Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 20л{r^3}}
To calculate the volume of ice-cream in cylindrical container
=Failed to parse (syntax error): {\displaystyle л{r^2}h}
= л X6X6X15
=540лc
Part 3 :
To apply condition given in the problem
volume of 10 cone with hemispherical top= volume of cylindrical container
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 20л{r^3}}
=540л
=Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {\frac{540л}{20л}}}
=27
r=3cm
Hence the radius of cream cones=3cm









