Difference between revisions of "Kepler's Laws"
| Line 25: | Line 25: | ||
[[Image:Gravitation%20for%20wiki_html_m290004f7.gif]] <br> | [[Image:Gravitation%20for%20wiki_html_m290004f7.gif]] <br> | ||
| − | G | + | <math>G m_1*M_s / r^12 = m_1*(v^12)/ r_1</math> |
| − | + | <math>v_1 = 2πr_1/T_1</math> | |
Substituting and rearranging we get | Substituting and rearranging we get | ||
| − | + | <math>T_12/r_13 = 4π^2/G*M_s</math> | |
Deriving this for another planet, we can arrive at the third law.<br><br> | Deriving this for another planet, we can arrive at the third law.<br><br> | ||
Revision as of 11:30, 4 December 2013
The Law of Orbits
All planets move in elliptical orbits, with the sun at one focus. An ellipse is a closed curve such that the sum of the distances from any point P on the curve to two fixed points (called the foci, F1 and F2) remains constant.
Orbit eccentricity
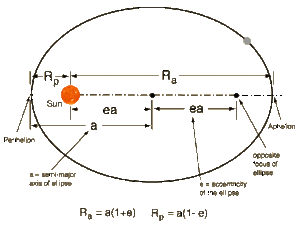
The semi major axis of the ellipse is a and represents the planet's average distance from the Sun. The eccentricity, “e” is defined so that “ea” is the distance from the centre to either focus. A circle is a special case of an ellipse where the two foci coincide. The Earth and most of the other planets have nearly circular orbits. For Earth, “e” = 0.017.
The Law of Equal Areas
Kepler's second law states that each planet moves so that an imaginary line drawn from the Sun to the planet sweeps out equal areas in equal periods of time. This can be shown to be true using the law of conservation of angular momentum.

If “v” is the velocity of the planet, in time “dt” the planet moves a distance vdt and sweeps out an area equal to the area of a triangle of base “r” and altitude vdt sinα.
Hence dA = ½ (r) (“v” x “dt” x sinα) dA/ dt = ½ rv sinα The magnitude of the angular momentum of the planet about the Sun is L = mvr sinα. dA/ dt = (½)L/m
Because the angular momentum is conserved, the rate of change of area covered is constant. This means that the planets move with different velocities depending upon their position in the orbits.
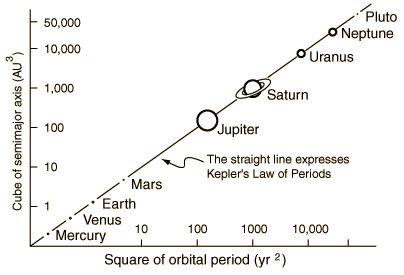
The Law of Periods
The ratio of the squares of the periods of any two planets revolving about the Sun is equal to the ratio of the cubes of their semi-major axes. Can you derive this?
Failed to parse (syntax error): {\displaystyle v_1 = 2πr_1/T_1}
Substituting and rearranging we get
Failed to parse (syntax error): {\displaystyle T_12/r_13 = 4π^2/G*M_s}
Deriving this for another planet, we can arrive at the third law.