Inverse Square Law
Newton's law of gravitation resembles Coulomb's law of electrical forces, which is used to calculate the magnitude of electrical force between two charged bodies. Both are inverse-square laws, in which force is inversely proportional to the square of the distance between the bodies. Coulomb's Law has the product of two charges in place of the product of the masses, and the electrostatic constant in place of the gravitational constant. One important point of comparison is that the the value of the constant in Coulomb's law (for force between two charges of 1C separated by a distance of 1 m) is of the order of magnitude 109, which is 1000 billion billion times more than the gravitational constant. This means that the electrostatic force is a much stronger force than the gravitational force.
Why should this be so?
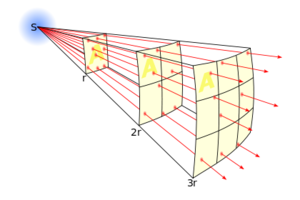
When we consider the gravitational field of a mass, we consider it to be a point mass. For any object, this can be approximated and we can find that this holds true. Some standard physics textbooks will give us this mathematical derivation as well. If there is a point mass and there is a field originating from it, the field must originate uniformly in all directions. If we imagine enclosing this point mass in a sphere and if we represent the field by field lines (called flux), we can visualize that these field lines must pass through uniformly throughout the surface area of the sphere. Now we can use simple geometry to explain why the field varies with inverse square of the distance. For the same area, the number of flux lines that will cut through a given area will reduce the farther the area is from the source. If we consider the area as a square on the surface of a sphere, the density of flux lines that will cut through the surface of a sphere is inversely proportional to the square of the distance from the source as the surface area of a sphere increases with the square of the radius. Hence the field strength will vary inversely with the square of the distance.