Difference between revisions of "Connection between algebra and geometry through graphs of lines and curves"
| Line 51: | Line 51: | ||
'''The above activity can also be done in a class room by asking to find coordinates of each student's position'''<br> | '''The above activity can also be done in a class room by asking to find coordinates of each student's position'''<br> | ||
| − | ==Activity 2== | + | ===Activity 2=== |
# '''Idea of introducing to coordinates - Activity No2''' | # '''Idea of introducing to coordinates - Activity No2''' | ||
[[http://tube.geogebra.org/material/show/id/147058 Play with the geogebra applet to familiarise with coordinates]] | [[http://tube.geogebra.org/material/show/id/147058 Play with the geogebra applet to familiarise with coordinates]] | ||
Revision as of 06:44, 14 August 2015
_
| Philosophy of Mathematics |
While creating a resource page, please click here for a resource creation checklist.
Concept Map
Textbook
Please click here for Karnataka and other text books.
Additional Information
Useful websites
Reference Books
Teaching Outlines
Connection between algebra and geometry through graphs of lines and curves
Learning objectives
- connection between algebra and geometry through graphs of lines and curves.
- Enabling geometric problems to be solved algebraically
- Geometrically visualising algebra
- introducing to the Cartesian coordinate plane
- plotting points on the plane
- reading coordinates for a point from a graph
Notes for teachers
A plane is a flat surface which can be extended in any directions
coordinate geometry gives us a way to describe a point on the plane exactly by two numbers.
Activity 1
- Familiarising to Cartesian Coordinate system - Activity No 1 [This source taken from mathopenref.com]
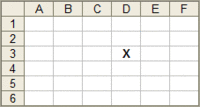
To introduce the idea, consider the grid on the right. The columns of the grid are lettered A,B,C etc. The rows are numbered 1,2,3 etc from the top. We can see that the X is in box D3; that is, column D, row 3.
D and 3 are called the coordinates of the box. It has two parts: the row and the column. There are many boxes in each row and many boxes in each column. But by having both we can find one single box, where the row and column intersect.
The above activity can also be done in a class room by asking to find coordinates of each student's position
Activity 2
- Idea of introducing to coordinates - Activity No2
[Play with the geogebra applet to familiarise with coordinates]
Concept #
Learning objectives
Notes for teachers
These are short notes that the teacher wants to share about the concept, any locally relevant information, specific instructions on what kind of methodology used and common misconceptions/mistakes.
Activities
- Activity No #1 Concept Name - Activity No.
- Activity No #2 Concept Name - Activity No.