Circles Tangents Problems
Problem 1
Tangents AP and AQ are drawn to circle with centre O, from an external point A. Prove that ∠PAQ=2.∠ OPQ
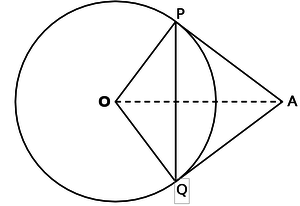
Interpretation of the problem
- O is the centre of the circle and tangents AP and AQ are drawn from an external point A.
- OP and OQ are the radii.
- The students have to prove thne angle PAQ=twise the angle OPQ.
Geogebra file
Concepts used
- The radii of a circle are equal.
- In any circle the radius drawn at the point of contact is perpendicular to the tangent.
- The tangent drawn from an external point to a circle a] are equal b] subtend equal angle at the centre c] are equally inclined to the line joining the centre and extrnal point.
- Properties of isoscles triangle.
- Properties of quadrillateral ( sum of all angles) is 360 degrees
- Sum of three angles of triangle is 180 degrees.
Algorithm
OP=OQ ---- radii of the same circle
OA is joined.
In quadrillateral APOQ ,
∠APO=∠AQO= [radius drawn at the point of contact is perpendicular to the tangent]
∠PAQ+∠POQ=
Or, ∠PAQ+∠POQ=
∠PAQ = -∠POQ ----------1
Triangle POQ is isoscles. Therefore ∠OPQ=∠OQP
∠POQ+∠OPQ+∠OQP=
Or ∠POQ+2∠OPQ=
2∠OPQ=- ∠POQ ------2
From 1 and 2
∠PAQ=2∠OPQ
Problem-2
In the figure two circles touch each other externally at P. AB is a direct common tangent to these circles. Prove that
a). Tangent at P bisects AB at Q
b). ∠APB=90° (Exescise-15.2, B.3)

Interpretation of the problem
- In the given figure two circles touch externally.
- AB is the direct common tangent to these circles.
- PQ is the transverse common tangent drawn to these circles at point P.
- Using the tangent properties students have to show AQ=BQ and ∠APB=90°
Concepts used
- The tangent drawn from an external point to a circle
a) are equal
b] subtend equal angle at the center
c] are equally inclined to the line joining the center and external point. - Angle subtended by equal sides are equal.
- Axiom-1:- "Things which are equal to same thing are equal"
[Click here for geogebra animation]
Algorithm
In the above figure AB is direct common tangent to two circles and PQ is the Transverse common tangent.
'Step-1'Bold text
AQ=QP and BQ=QP (Tangents drawn from external point are equal)
By axiom-1, AQ=BQ
∴tangent at P bisects AB at Q.
problem 3 [Ex-15.2 B.7]
Circles and touch internally at a point A and AB is a chord of the circle intersecting at P, Prove that AP= PB.
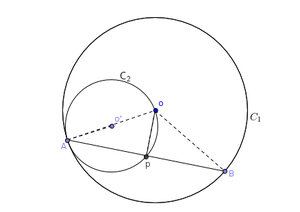
Concepts used
- The radii of a circle are equal
- Properties of isosceles triangle.
- SAS postulate
- Properties of congruent triangles.
Prerequisite knowledge
- The radii of a circle are equal.
- In an isosceles triangle angles opposite to equal sides are equal.
- All the elements of congruent triangles are equal.
Algoritham
In ∆AOB
AO=BO [Radii of a same circle]
∴ ∠OAB = ∠OBA --------------I [∆AOB is an isosceles ∆}
Then,
In ∆AOP and ∆BOP,
AO = BO [Radii of a same circle]
OP=OP [common side]
∠OAP = ∠OBP [ from I]
∴ ∆AOP ≅ ∆BOP [SAS postulate]
∴ AP = BP [corresponding sides of congruent triangles ]



