Difference between revisions of "Circles Tangents Problems"
dimpugirish (talk | contribs) |
m (added Category:Circles using HotCat) |
||
| (38 intermediate revisions by 5 users not shown) | |||
| Line 7: | Line 7: | ||
#The students have to prove thne angle PAQ=twise the angle OPQ. | #The students have to prove thne angle PAQ=twise the angle OPQ. | ||
===Geogebra file=== | ===Geogebra file=== | ||
| − | < | + | <span> </span> |
| + | |||
| + | <span></span><div id="ggbContainer14a2b70cb23c6cb8374fd4f22e997e08"></div><span></span> | ||
==Concepts used== | ==Concepts used== | ||
| Line 46: | Line 48: | ||
==Algorithm== | ==Algorithm== | ||
In the above figure AB is direct common tangent to two circles and PQ is the Transverse common tangent.<br> | In the above figure AB is direct common tangent to two circles and PQ is the Transverse common tangent.<br> | ||
| − | + | a)<br> | |
AQ=QP and BQ=QP (Tangents drawn from external point are equal)<br> | AQ=QP and BQ=QP (Tangents drawn from external point are equal)<br> | ||
By axiom-1, AQ=BQ<br> | By axiom-1, AQ=BQ<br> | ||
| − | ∴tangent at P bisects AB at Q. | + | ∴tangent at P bisects AB at Q.<br> |
| + | b)<br> | ||
| + | Let ∠QBP=x˚<br> | ||
| + | |||
| + | ∴∠QPB=x˚ (∵PQ=BQ)<br> | ||
| + | Now Let ∠PAQ=y˚<br> | ||
| + | ∠QPA=y˚ (∵ PQ=AQ)<br> | ||
| + | ∴In △PAB<br> | ||
| + | |||
| + | ∠PAB+∠PBA+∠APB=180˚<br> | ||
| + | |||
| + | y˚+x˚+(x˚+y˚)=180˚<br> | ||
| + | 2x˚+2y˚=180˚<br> | ||
| + | 2(x˚+y˚)=180˚<br> | ||
| + | x˚+y˚=90˚<br> | ||
| + | ∴ ∠APB=90˚ | ||
| + | |||
=problem 3 [Ex-15.2 B.7]= | =problem 3 [Ex-15.2 B.7]= | ||
Circles <math>C_{1}</math> and <math>C_{2}</math> touch internally at a point A and AB is a chord of the circle<math>C_{1}</math> intersecting <math>C_{2}</math> at P, Prove that AP= PB.<br> | Circles <math>C_{1}</math> and <math>C_{2}</math> touch internally at a point A and AB is a chord of the circle<math>C_{1}</math> intersecting <math>C_{2}</math> at P, Prove that AP= PB.<br> | ||
| Line 79: | Line 97: | ||
'''In the given Quadrilateral ABCD , BC=38cm , QB=27cm , DC=25cm and AD⊥DC find the radius of the circle.(Ex:15.2. A-6)'''<br> | '''In the given Quadrilateral ABCD , BC=38cm , QB=27cm , DC=25cm and AD⊥DC find the radius of the circle.(Ex:15.2. A-6)'''<br> | ||
[[File:fig3.png|200px]] | [[File:fig3.png|200px]] | ||
| + | ==Interpretation of problem== | ||
| + | # In the quadrilateral ABCD sides BC , DC & QB are given . | ||
| + | #AD⊥DC. | ||
| + | # Asked to find the radius OS or OP | ||
| + | |||
| + | ==Concepts used== | ||
| + | #Tangents drawn from an external point to a circle are equal. | ||
| + | #In a quadrilateral, if all angles are equal and a pair of adjacent sides are equal then it is a square | ||
| + | #In a circle, the radius drawn at the point of contact is perpendicular to the tangent | ||
| + | ==Algorithm== | ||
| + | In the fig BC=38 cm and BQ=27 cm <br> | ||
| + | BQ=BR=27 cm (∵ by concept 1) <br> | ||
| + | ∴CR=BC-BR=38-27=11 cm <br> | ||
| + | CR=SC=11 cm (∵ by concept 1) <br> | ||
| + | DC=25 cm <br> | ||
| + | ∴ DS=DC-SC=25-11=14 cm <br> | ||
| + | DS=DP=14 cm (∵ by concept 1) <br> | ||
| + | Also AD⊥DC, OP ⊥ AD and OS ⊥ DC <br> | ||
| + | ∠D=∠S=∠P=90˚ <br> | ||
| + | ⇒ ∠O=90˚ <br> | ||
| + | ∴ DSOP is a Square <br> | ||
| + | SO=OP=14 cm <br> hence Radius of given circle is 14 cm | ||
| + | |||
| + | =Problem 5 [Ex-15.2-B8]= | ||
| + | A circle is touching the side BC of △ABC at P. AB and AC when produced are touching the circle at Q and R respectively. Prove that AQ =<math>\frac{1}{2}</math> [perimeter of △ABC]. | ||
| + | [[File:123.png|300px]] | ||
| + | |||
| + | ==Algorithm== | ||
| + | In the figure AQ , AR and BC are tangents to the circle with center O.<br> | ||
| + | BP=BQ and PC=CR (Tangents drawn from external point are equal) ---------- (1)<br> | ||
| + | |||
| + | Perimeter of △ABC=AB+BC+CA<br> | ||
| + | =AB+(BP+PC)+CA<br> | ||
| + | =AB+BQ+CR+CA ------ (From eq-1)<br> | ||
| + | =(AB+BQ)+(CR+CA)<br> | ||
| + | =AQ+AR ----- (From fig)<br> | ||
| + | =AQ+AQ -- --- (∵AQ=AR)<br> | ||
| + | =2AQ<br> | ||
| + | |||
| + | ∴ AQ = <math>\frac{1}{2}</math> [perimeter of △ABC] | ||
| + | |||
| + | =Problem-6 [Ex-15.4-B3]= | ||
| + | In circle with center O , diameter AB and a chord AD are drawn. Another circle drawn with OA as diameter to cut AD at C. Prove that BD=2OC.[[File:15.4B3.png|300px]] | ||
| + | ==Algorithm== | ||
| + | In figure, AB is the diameter of circle <math>C_{1}</math> and AO is the diameter of the circle <math>C_{2}</math><br>in △ADB and △ACO<br> | ||
| + | ∠ADB=90° and ∠ACO=90° [∵angles in the semi circles]<br>∠DAB=∠CAO [∵common angles]<br>∴△ADB∼△ACO [∵equiangular triangles are similar]<br>∴<math>\frac{AB}{OA}</math>=<math>\frac{BD}{OC}</math>=<math>\frac{AD}{AC}</math> [∵corresonding sides of a similar triangles are proportional]<br>But AB=2OA----1 (∵diameter is twice the radius of a cicle)<br><math>\frac{AB}{OA}</math>=<math>\frac{BD}{OC}</math><br>from (1)<br><math>\frac{2OA}{OA}</math>=<math>\frac{BD}{OC}</math><br>∴BD=2OC | ||
| + | |||
| + | |||
| + | |||
| + | =Problem-7 [Ex-15.4-A3]= | ||
| + | |||
| + | In the figure AB=10cm,AC=6cm and the radius of the smaller circle is xcm. find x. | ||
| + | |||
| + | [[File:circle.png|400px]] | ||
| + | |||
| + | ==Interpretation of the problem== | ||
| + | #In the given figure two circles touch internally. | ||
| + | #OB and OF are the radii of the semicircle with center "O". | ||
| + | #PC and PF are the radii of the circle with center "P". | ||
| + | |||
| + | ==Ex 4.4.2== | ||
| + | #Suppose two chords of a circle are equidistant from the centre of the circle, prove that the chords have equal length. | ||
| + | '''DATA''' :- Let AB & CD are the two chords which are equidistant from the centre 'O' of the circle. [ Here OP is the perpendicular distance from the centre O to the chord AB and OQ is the perpendicular distance from the centre O to the chord CD] OP = OQ. | ||
| + | |||
| + | '''TO PROVE :-''' AB = CD, | ||
| + | |||
| + | '''CONSTRUCTION :-''' Join OA & OD. | ||
| + | |||
| + | '''PROOF :-''' | ||
| + | {[Consider In ∆AOP & ∆DOQ OA = OD OP = OQ Angle APO = Angle DQO ∆AOP ≡ ∆DOQ AP = DQ Let AB = AP + BP = AP + AP = 2AP AB = 2DQ ---------- 1. and CD = CQ + DQ = DQ + DQ CD = 2DQ --------- 2. From equtn 1 & equtn 2 AB = CD | ||
| + | Radii of the circle Equi distances from circle | ||
| + | SAS Axiom | ||
| + | Acording to properties of SAS axiom. | ||
| + | |||
| + | Perpendicular drawn from centre to chord which bisect the chord, i.e. AP = BP. | ||
| + | |||
| + | Perpendicular drawn from centre to chord which bisect the chord, i.e. CQ = DQ Acording to AXIOM-1]} | ||
| + | |||
| + | angle | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | |'''Steps''' | ||
| + | |'''Explanation''' | ||
| + | |- | ||
| + | |[[Image:solution.png|300px|link=http://karnatakaeducation.org.in/KOER/en/index.php/File:Solution.png]] | ||
| + | |Explanation for thestep | ||
| + | |- angle | ||
| + | |Write the step | ||
| + | |Explanation for thestep | ||
| + | |}|} | ||
| + | |||
| + | [[Category:Circles]] | ||
Latest revision as of 11:42, 29 October 2019
Problem 1
Tangents AP and AQ are drawn to circle with centre O, from an external point A. Prove that ∠PAQ=2.∠ OPQ
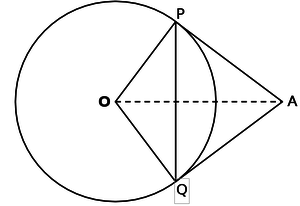
Interpretation of the problem
- O is the centre of the circle and tangents AP and AQ are drawn from an external point A.
- OP and OQ are the radii.
- The students have to prove thne angle PAQ=twise the angle OPQ.
Geogebra file
Concepts used
- The radii of a circle are equal.
- In any circle the radius drawn at the point of contact is perpendicular to the tangent.
- The tangent drawn from an external point to a circle a] are equal b] subtend equal angle at the centre c] are equally inclined to the line joining the centre and extrnal point.
- Properties of isoscles triangle.
- Properties of quadrillateral ( sum of all angles) is 360 degrees
- Sum of three angles of triangle is 180 degrees.
Algorithm
OP=OQ ---- radii of the same circle
OA is joined.
In quadrillateral APOQ ,
∠APO=∠AQO= [radius drawn at the point of contact is perpendicular to the tangent]
∠PAQ+∠POQ=
Or, ∠PAQ+∠POQ=
∠PAQ = -∠POQ ----------1
Triangle POQ is isoscles. Therefore ∠OPQ=∠OQP
∠POQ+∠OPQ+∠OQP=
Or ∠POQ+2∠OPQ=
2∠OPQ=- ∠POQ ------2
From 1 and 2
∠PAQ=2∠OPQ
Problem-2
In the figure two circles touch each other externally at P. AB is a direct common tangent to these circles. Prove that
a). Tangent at P bisects AB at Q
b). ∠APB=90° (Exescise-15.2, B.3)

Interpretation of the problem
- In the given figure two circles touch externally.
- AB is the direct common tangent to these circles.
- PQ is the transverse common tangent drawn to these circles at point P.
- Using the tangent properties students have to show AQ=BQ and ∠APB=90°
Concepts used
- The tangent drawn from an external point to a circle
a) are equal
b] subtend equal angle at the center
c] are equally inclined to the line joining the center and external point. - Angle subtended by equal sides are equal.
- Axiom-1:- "Things which are equal to same thing are equal"
[Click here for geogebra animation]
Algorithm
In the above figure AB is direct common tangent to two circles and PQ is the Transverse common tangent.
a)
AQ=QP and BQ=QP (Tangents drawn from external point are equal)
By axiom-1, AQ=BQ
∴tangent at P bisects AB at Q.
b)
Let ∠QBP=x˚
∴∠QPB=x˚ (∵PQ=BQ)
Now Let ∠PAQ=y˚
∠QPA=y˚ (∵ PQ=AQ)
∴In △PAB
∠PAB+∠PBA+∠APB=180˚
y˚+x˚+(x˚+y˚)=180˚
2x˚+2y˚=180˚
2(x˚+y˚)=180˚
x˚+y˚=90˚
∴ ∠APB=90˚
problem 3 [Ex-15.2 B.7]
Circles and touch internally at a point A and AB is a chord of the circle intersecting at P, Prove that AP= PB.
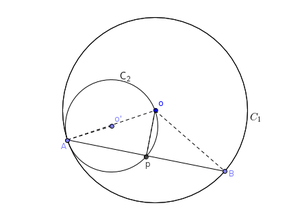
Concepts used
- The radii of a circle are equal
- Properties of isosceles triangle.
- SAS postulate
- Properties of congruent triangles.
Prerequisite knowledge
- The radii of a circle are equal.
- In an isosceles triangle angles opposite to equal sides are equal.
- All the elements of congruent triangles are equal.
Algoritham
In ∆AOB
AO=BO [Radii of a same circle]
∴ ∠OAB = ∠OBA --------------I [∆AOB is an isosceles ∆}
Then,
In ∆AOP and ∆BOP,
AO = BO [Radii of a same circle]
OP=OP [common side]
∠OAP = ∠OBP [ from I]
∴ ∆AOP ≅ ∆BOP [SAS postulate]
∴ AP = BP [corresponding sides of congruent triangles ]
problem-4
In the given Quadrilateral ABCD , BC=38cm , QB=27cm , DC=25cm and AD⊥DC find the radius of the circle.(Ex:15.2. A-6)
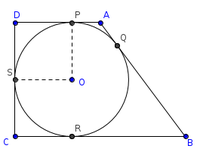
Interpretation of problem
- In the quadrilateral ABCD sides BC , DC & QB are given .
- AD⊥DC.
- Asked to find the radius OS or OP
Concepts used
- Tangents drawn from an external point to a circle are equal.
- In a quadrilateral, if all angles are equal and a pair of adjacent sides are equal then it is a square
- In a circle, the radius drawn at the point of contact is perpendicular to the tangent
Algorithm
In the fig BC=38 cm and BQ=27 cm
BQ=BR=27 cm (∵ by concept 1)
∴CR=BC-BR=38-27=11 cm
CR=SC=11 cm (∵ by concept 1)
DC=25 cm
∴ DS=DC-SC=25-11=14 cm
DS=DP=14 cm (∵ by concept 1)
Also AD⊥DC, OP ⊥ AD and OS ⊥ DC
∠D=∠S=∠P=90˚
⇒ ∠O=90˚
∴ DSOP is a Square
SO=OP=14 cm
hence Radius of given circle is 14 cm
Problem 5 [Ex-15.2-B8]
A circle is touching the side BC of △ABC at P. AB and AC when produced are touching the circle at Q and R respectively. Prove that AQ = [perimeter of △ABC].
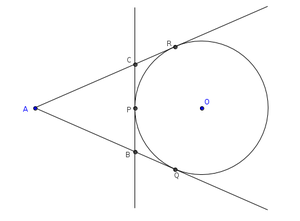
Algorithm
In the figure AQ , AR and BC are tangents to the circle with center O.
BP=BQ and PC=CR (Tangents drawn from external point are equal) ---------- (1)
Perimeter of △ABC=AB+BC+CA
=AB+(BP+PC)+CA
=AB+BQ+CR+CA ------ (From eq-1)
=(AB+BQ)+(CR+CA)
=AQ+AR ----- (From fig)
=AQ+AQ -- --- (∵AQ=AR)
=2AQ
∴ AQ = [perimeter of △ABC]
Problem-6 [Ex-15.4-B3]
In circle with center O , diameter AB and a chord AD are drawn. Another circle drawn with OA as diameter to cut AD at C. Prove that BD=2OC.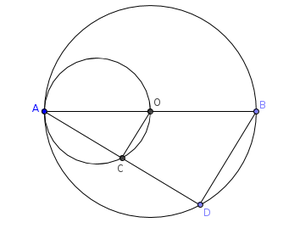
Algorithm
In figure, AB is the diameter of circle and AO is the diameter of the circle
in △ADB and △ACO
∠ADB=90° and ∠ACO=90° [∵angles in the semi circles]
∠DAB=∠CAO [∵common angles]
∴△ADB∼△ACO [∵equiangular triangles are similar]
∴== [∵corresonding sides of a similar triangles are proportional]
But AB=2OA----1 (∵diameter is twice the radius of a cicle)
=
from (1)
=
∴BD=2OC
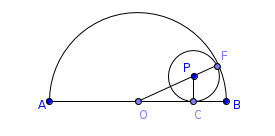
Problem-7 [Ex-15.4-A3]
In the figure AB=10cm,AC=6cm and the radius of the smaller circle is xcm. find x.
Interpretation of the problem
- In the given figure two circles touch internally.
- OB and OF are the radii of the semicircle with center "O".
- PC and PF are the radii of the circle with center "P".
Ex 4.4.2
- Suppose two chords of a circle are equidistant from the centre of the circle, prove that the chords have equal length.
DATA :- Let AB & CD are the two chords which are equidistant from the centre 'O' of the circle. [ Here OP is the perpendicular distance from the centre O to the chord AB and OQ is the perpendicular distance from the centre O to the chord CD] OP = OQ.
TO PROVE :- AB = CD,
CONSTRUCTION :- Join OA & OD.
PROOF :-
{[Consider In ∆AOP & ∆DOQ OA = OD OP = OQ Angle APO = Angle DQO ∆AOP ≡ ∆DOQ AP = DQ Let AB = AP + BP = AP + AP = 2AP AB = 2DQ ---------- 1. and CD = CQ + DQ = DQ + DQ CD = 2DQ --------- 2. From equtn 1 & equtn 2 AB = CD
Radii of the circle Equi distances from circle
SAS Axiom
Acording to properties of SAS axiom.
Perpendicular drawn from centre to chord which bisect the chord, i.e. AP = BP.
Perpendicular drawn from centre to chord which bisect the chord, i.e. CQ = DQ Acording to AXIOM-1]}
angle
| Steps | Explanation |
|
Explanation for thestep |
| Write the step | Explanation for thestep |
|}