Newton's Law of Gravitation
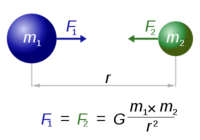
Newton's Law of Gravitation Newton's law of universal gravitation states that every particle in the universe attracts every other particle with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between them. This force acts along the line joining the two particles. Separately it was shown that large spherically symmetrical masses attract and are attracted as if all their mass were concentrated at their centres.
For non-symmetric objects, the masses will be concentrated a the centre of mass and the distance between these centres is what will be taken as the distance
F = G m_1*m_2 / r^2
- F is the force between the masses,
- m1 is the first mass,
- m2 is the second mass,
- G is the gravitational constant
- r is the distance between the masses
In SI units, Force, F is measured in newtons (N), masses m1 and m2 are measured in kilograms (kg), and the distance between the masses is measured in metres.
Universal Gravitational Constant
The magnitude of G is identical to the magnitude of the force between a pair of 1-kg masses that are 1 metre apart and has been experimentally determined to be equal to 6.674×10−11N m2 kg−2. The value of the constant G was first accurately determined from the results of an experiment conducted by the British scientist Henry Cavendish in 1798. He accomplished by measuring the tiny force between lead masses with an extremely sensitive torsion balance. This small magnitude indicates that the gravitational force is an extremely weak force.
This experiment was also the first test of Newton's theory of gravitation between masses in the laboratory. It took place 111 years after the publication of Newton's Principia and 71 years after Newton's death, so none of Newton's calculations could use the value of G; instead he could only calculate a force relative to another force.