Hopping on number line
Activity - Number Line introduction
Objectives
- Represent the number line using objects.
- Count each group of ones objects.
- Relate the cumulative total of each group to the number on the number line. Write the cumulative total for each group.
- Skip count by pointing to each group of objects.
Estimated Time
This is a lesson and could take 3-4 periods.
Materials/ Resources needed
Paper, Pencil, Chalk, Large Room in which number line can be formed
Prerequisites/Instructions, if any
Multimedia resources
Website interactives/ links/ simulations/ Geogebra Applets
Process (How to do the activity)
Introduction
- Number line activity to be done in class with positive numbers and then followed with this set of worksheets. Make 2x2 sets of numbers – positive and negative - (-7,-6,-5,.....,5,6,7,8,9,10)
- Ask them to arrange the 1st set of cards. Give them positive numbers in the first activity.
- They should know the increasing order of number line
- We know that they are familiar with number line
- When you add 1, where do you go?
- When you add 0, where do you go? (Additive identity)
The number line in teaching mathematics
One reason to use this mathematical object with students is that they need to see arithmetic in both contexts: counting and measuring. At the beginning, children may sometimes use the number line to find answers to arithmetic problems (e.g., figuring out what 3 + 10 is, before that becomes automatic to them) but that is never its purpose. We don’t rely on the number line for getting answers -- for that, we want the children to know basic facts and methods and use their heads -- but we do use the number line to understand things about the operation (addition and subtraction) and to understand what the answers mean. For example, the answer to the subtraction problem 92 – 49 is the distance between those two numbers on the number line. That image can greatly help mental computation: 49 to 50 is one step, 50 to 90 is another forty steps, and 90 to 92 is another two steps, so altogether 43 steps. (See number line addition and subtraction below.) It also makes arithmetic with negetive numbers which has been already discussed. And the number line is essential for full understanding of fractions and decimals. In fact, a ruler (a number line!) is one of the important places students encounter and need to use fractions.
In counting
Number lines are first used just to show sequence—numbers standing on line in order! At this stage, neither the straightness of the line nor the distance between numbers is mathematically important, though our images are always standard anyway. Children will look at chunks of the line, not always starting at 1, and will work forwards or backwards from some number that is placed on the line. They are learning about sequence and order, and that develops somewhat independently from counting.
In measurement
Students also learn about intervals on the number line, but just begin that process. Kids used to gain the interval idea (in a slightly different form) from their experience playing board games. They knew that when they rolled a 5, they had to count their five spaces beginning with the next space. That is, they were counting moves, not positions. Measurement depends on it. Addition and subtraction with counters does not depend on it, but those operations on the number line do depend on it.
Addition and Subtraction using number line
If we can add and subtract with counters, why use the number line? To connect these operations with measurement, and also because the counters no longer suffice when we get to fractions, decimals, and negative numbers. Over time, kids will connect number line images with thermometers, clocks, rulers (with fractional inches)… Coordinate graphs are based on perpendicular number lines; even bar graphs require the measurement idea more than the count idea, although they can begin with count. Addition and subtraction, or comparison, of distance is also why we use number lines. Adding distance is further developed on open number lines. Students develop many ways to subtract (in second grade, they learn to subtract 8 from anything by subtracting 10 and then compensating, and then they extend that idea to other additions and subtractions).
Objectives
- Ask children to move places along the number line by adding positions; by subtracting positions
- Encouraging students to come to the number line and skip count by ones pointing to the numbers on the number line that represent each one.
- Addition of positive numbers by moving along number line
- Subtraction of positive numbers by moving along number line
- They should formulate this as a word problem
Sum and product of numbers
Objectives
- Using the number line model to find sum and products
- Solving and creating puzzles using the number line
- Investigating the order property of addition and multiplication
Materials
Counters for the number line (chips, markers, etc.)
How to do the activity(addition)
Tell the students that they will find sums using the number line model. Then display a large number line and a 5+4 pencils , that is, a pencil with 5 spots on the left side and 4 spots on the right. Then demonstrate with a counter how a hop of 5 is taken on the number line. You may wish to encourage students to count aloud as the hop is made. Then make a hop of 4, starting at the place the counter landed. You might choose to have them record what happened using the equation notation 5 + 4 = 9, or to informally describe the moves this way: “If you take a hop of 5 spaces and then a hop of 4 spaces, you land on 9.” You may wish to highlight the fact that in this model, spaces are counted, not points on the number line.
Questions for discussion
- Which number did you land on when you made a 5-hop, then a 3-hop? Could you land on the same number if you took a 3-hop first, then a 5-hop? How do you know?
The answers could be yes [ 5 + 3 = 8, and 3 + 5 = 8.]. Laws of computation can be introduced.
- What sums did you model with hops? How did you record them? [Student responses will depend upon the "hops" they performed.]
- Were any of the sums the same? Why? [Student responses will depend upon the "hops" they performed.]
- How would you find the sum of 2 and 5? [Make a hop of 2, and then a hop of 5, to reach 7.]
- How would you tell a friend to add on the number line?
- How is using a number line like measuring? How is it different?
- Which students counted as they took hops and which moved directly to the number?
Negative numbers on number line and operation on number lines
- Increasing order of number line
- Addition of positive numbers
- Subtraction of positive numbers
- Addition and subtraction are opposite operations
- Negative numbers are opposite of positive numbers
- They do the opposite; when you add a negative number, you go backward in the number line
- When you subtract a negative number, you go forward.
- Distinguish between
5 – 3 and 5 + (-3)
- Show the operations on negative numbers (addition, subtraction, multiplication if possible)
Hopping Number Line
In this lesson, students generate sums using the number line model. This model highlights the measurement aspect of addition and is a distinctly different representation of the operation from the model presented in the previous discussion. The order (commutative) property is also introduced. At the end of the lesson, students are encouraged to predict sums and to answer puzzles involving addition.
Objectives
- Represent the number line using objects.
- Count each group of ones objects.
- Relate the cumulative total of each group to the number on the number line. Write the cumulative total for each group.
- Skip count by pointing to each group of objects.
How to do the activity
- Discuss a sample problem like this. Ram and his dad are driving to the city. It is 15 kms away. They have already gone 5 kms. How many more kms do they have to drive?
After a minute or so, ask for a few children to share with the class. You have to figure out how much farther they have to drive. You could keep going, like count up from 5 to 15. You could go maybe go backwards from 15 down to 5. Students will probably have a variety of ideas for solving the problem, including counting on from, or adding to 5 to reach 15, or counting backwards from 15 to find out how many kms remain.
- Summarize both approaches by writing the following equations below:
5 + □ = 15
15 – □ = 5
- We could say we just keep going from 5 up to 15, so we wrote 5 + box equals 15. What does the box mean in this equation? The students may say it means part you have to figure out. It’s where you write the answer. It’s like the problem you have to solve. 5 plus how many more to get to 15?
- Another interpretation is that it is like you’re finding out how far you have to go backwards to get down to 5. This is the idea that subtraction is the inverse process of addition.
- After taking students’ ideas, it is possible to introduce number lines as a new tool for solving problems like these. Number line can be drawn as a horizontal line across the board. *Include an arrow on either end to show that the number line continues indefinitely in both directions. Record the smaller number (5) by marking and labeling a dot on the far left side. Then propose to move along the number line by hops greater than 1 to find the difference between 5 and 15.
- This discussion can be extended with the following question. What if Ram and his dad drive 2 more kms? How far will they be then? This can also be shown on the number line. What if they drove 3 more kms after that? How far would they be? The students should be able to say they are upto 10 miles!
They have gone 5 miles after the 5 because 2+3=5 and it is possible to know how many more miles they have to go to get to 15!
- Ask students to suggest additional hops you could take along the number line to get to 15.
You could keep going by ones, like 1 and then 2and so on more little hop up to 15.

And this can be generalized for negative numbers also.
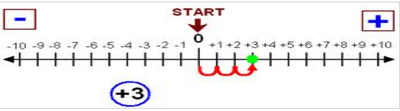
- Addition and subtraction are opposite operations
Evaluation (Questions for assessment of the child)
- How much farther did Ram and his dad have to drive to get to the city?
- How do you know? Can you show us on the open number line?
- Does this give us the answer to the problem?
- Did we add or subtract to find the answer?
Worksheets
- Addition as going forward click here
- When you add 1 where do you go? (With and without the number line)click here
- Addition using number line click here
- Subtraction using number line click here
- Working problem on subtraction using number line click here
- For level one, concept of hopping on number line click here .
- For level 2 worksheet on hopping on the number line click here.
Question Corner
Activity Keywords
To link back to the concept page Numbers

